ОПРЕДЕЛЕНИЕ ШИРИНЫ РАСКРЫТИЯ ТРЕЩИН, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА

4.10.Ширину раскрытия нормальных трещин определяют по формуле

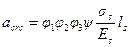(4.10)

где σ_s - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно п.4.11;

l_s - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами, определяемое согласно п.4.12;

ψ_s - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать ψ_s = 1; если при этом условие (4.1) не удовлетворяется, значение ψ_s следует определять согласно п.4.13;

φ₁- коэффициент, учитывающий продолжительность действия нагрузки и принимаемый равным:

1,0 - при непродолжительном действии нагрузки;

1,4 - при продолжительном действии нагрузки;

φ₂ - коэффициент, учитывающий профиль продольной арматуры и принимаемый равным:

0,5 - для арматуры периодического профиля (классов А300, А400, А500, В500);

0,8 - для гладкой арматуры (класса А240);

φ₃ - коэффициент, учитывающий характер нагружения и принимаемый равным:

1,0 - для изгибаемых и внецентренно сжатых элементов;

1,2 - для растянутых элементов.

4.11. Значение напряжения a_s в растянутой арматуре изгибаемых элементов (черт.4.2,а) определяют по формуле

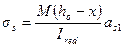(4.11)

где I_red и х - момент инерции и высота сжатой зоны приведенного поперечного сечения, включающего в себя площадь поперечного сечения только сжатой зоны бетона и площади сечения растянутой и сжатой арматуры, умноженные на коэффициент приведения арматуры к бетону 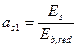, где Е_b,red - см. п.4.7.

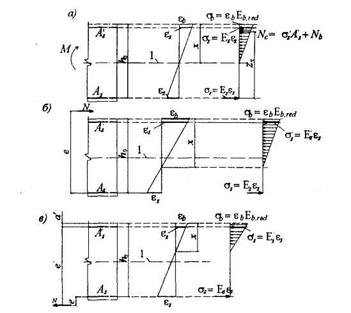
Черт.4.2. Схемы напряженно-деформированного состояния элементов с трещинами при действии: изгибающего момента (а), сжимающей продольно силы (б), растягивающей продольной силы (в)

1 -уровень центра тяжести приведенного сечения

Коэффициент a_s1 можно также определять по формуле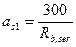

Высота сжатой зоны определяется из решения уравнения

S_b = a_s1 (S_s -S'_s), (4.12)

где S_b, S_s, S'_s - статические моменты соответственно сжатой зоны бетона, площадей растянутой и сжатой арматуры относительно нейтральной оси.

Для прямоугольных, тавровых и двутавровых сечений напряжение σ_s допускается определять по формуле

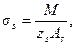(4.13)

где z_s - плечо внутренний пары сил, равное z_s = ζh_o, а коэффициент ζ, определяется по графику на черт.4.3.

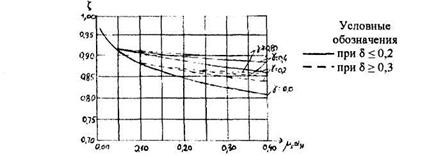
Черт.4.3. График коэффициента ζ = z_s /h_o для определения плеча внутренней пары сил при расчете по раскрытию трещин изгибаемых элементов

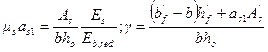, δ = h'_f /h_o для сечений без сжатой полки δ = 2a' /h_o

Значение напряжения σ_s для внецентренно сжатых элементов, а также для внецентренно растянутых элементов при приложении силы N вне расстояния между арматурами S и S' (черт.4.2,б, в)определяют по формуле

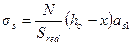(4.14)

где S_red - статический момент относительно нейтральной оси;значение S_red вычисляют по формуле

S_red = S_b + a_s1(S'_s - S_s), (4.15)

а высоту сжатой зоны х определяют из решения уравнения

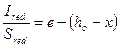, (4.16)

гдеI_red - момент инерции приведенного сечения относительно нейтральной оси.

Для внецентренно растянутых элементов эксцентриситет е в формуле (4.16) принимают со знаком "минус".

Значение напряжения σ_s для внецентренно растянутых элементов при приложении силы N между центрами тяжести арматуры S и S' (т.е. при е' < h_o - а) определяют по формуле

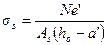(4.17)

Для центрально растянутых элементов

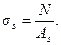(4.18)

Для внецентренно сжатых элементов прямоугольного сечения напряжение σ_s допускается определять по формуле

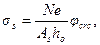(4.19)

где φ_сrс - коэффициент, определяемый по табл.4.2.

Для внецентренно растянутых элементов прямоугольного сечения напряжение σ_s допускается определять по формулам:

а) при е' > h_o – а' и при А'_s = 0 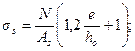(4.20)

б) при А'_s ≥ А_s независимо от е' 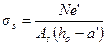. (4.21)

При 0 < А'_s < A_s значение σ_s определяется линейной интерполяцией между значениями σ_s вычисленными по формулам (4.20) и (4.21).

Во всех случаях значение σ_s не должно превышать R_s,_ser.

Таблица 4.2

e/ho	Коэффициенты φсrс
при А's ≥ As и значениях μas1,равных	при А's = 0 и значениях μa1, равных
0,01	0,05	0,10	0,20	≥0,40	0,01	0,05	0,10	0,20	≥0,40
≤0,8	0,01	0,06	0,07	0,08	0,08	0,01	0,06	0,10	0,20	0,18
1,0	0,13	0,20	0,23	0,25	0,26	0,13	0,20	0,26	0,31	0,36
1,2	0,25	0,33	0,37	0,39	0,40	0,25	0,33	0,38	0,43	0,49
1,5	0,42	0,48	0,52	0,54	0,55	0,42	0,48	0,53	0,58	0,64
2,0	0,56	0,63	0,66	0,68	0,69	0,56	0,63	0,67	0,72	0,78
3,0	0,73	0,79	0,82	0,84	0,85	0,73	0,79	0,82	0,88	0,93
4,0	0,80	0,86	0,90	0,93	0,93	0,80	0,86	0,91	0,96	1,01
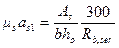
Примечание. При 0 < А's < As коэффициенты φсrс определяются линейной интерполяцией.

4.12. Значение базового расстояния между трещинами l_s определяется по формуле

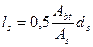(4.22)

и принимают не менее 10d_s и 100 мм и не более 40d_s и 400 мм (для элементов с рабочей высотой поперечного сечения не более 1 м).

Здесь A_bt - площадь сечения растянутого бетона, определяемая в общем случае согласно указаниям п.4.7. При этом высота растянутой зоны бетона принимается не менее 2а и не более 0,5h. Для прямоугольных, тавровых и двутавровых сечений высоту растянутой зоны бетона допускается определять по формуле (4.23) с учетом указанных ограничений:

y = y_tk (4.23)

где y_t - высота растянутой зоны бетона, определяемая как для упругого материала при коэффициенте приведения арматуры к бетону, а = Е_s/Е_ь;

к - поправочный коэффициент, равный:

для прямоугольных сечений и тавровых с полкой в сжатой зоне - 0,90;

для двутавровых (коробчатых) сечений и тавровых с полкой в растянутой зоне - 0,95. Значение y_t принимается равным:

для изгибаемых элементов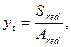

для внецентренно нагруженных элементов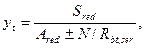

гдеS_red - статический момент полного приведенного сеченияотносительно растянутой грани;

А_red - см.формулу (4.8);

знак "плюс" принимается при сжимающей продольной силе N,

знак "минус" - при растягивающей силе N.

При различных диаметрах стержней растянутой арматуры значение d_s принимается равным

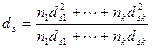, (4.24)

где d_s1... d_sk - диаметры стержней растянутой арматуры;

n₁...n_k - число стержней диаметрами соответственно d_s1... d_sk.

4.13. Значение коэффициента ψ_s определяют по формуле

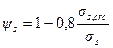, (4.25)

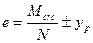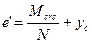где σ_s,_crc -напряжение в продольной растянутой арматуре в сечении сразу после образования нормальных трещин, определяемое по указаниям п.4.11, принимая в соответствующих формулах М = M_crc , и , где у_р и y_c - расстояния соответственно от центра тяжести растянутой и сжатой арматуры до оси, проходящей через центр тяжести приведенного сечения, принятого при определении M_crc;при этом знак " плюс" принимается при внецентренном сжатии, знак "минус" - при внецентренном растяжении; M_crc - см. пп.4.4-4.8; N -продольная сила при действии рассматриваемой нагрузки;

σ_s - напряжение в продольной растянутой арматуре, при действии рассматриваемой нагрузки.

Если σ_s,_crc > σ_s, принимают ψ_s = 0,2.

Для изгибаемых элементов значение коэффициента ψ_s, допускается определять по формуле

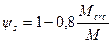, (4.26)

и принимать не менее 0,2.

4.14. Ширину раскрытия трещин принимают равной: при продолжительном раскрытии

a_crc = a_crc1 ; (4.27)

при непродолжительном раскрытии

a_crc = a_crc,1 + a_crc,2 - a_crc,3, (4.28)

где a_crc,1 - ширина раскрытия трещин, определяемая согласно п.4.10 при φ₁=1,4 и при действии постоянных и длительных нагрузок;

a_crc,2 - то же, при φ₁= 1,0 и действии всех нагрузок (т.е. включая кратковременные);

a_crc,3 - то же, при φ₁=1,0 и действии постоянных и длительных нагрузок.

Ширину непродолжительного раскрытия трещин можно также определять по формуле

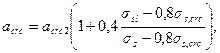(4.28а)

где значения σ_sl и σ_s определяются согласно п.4.11 при действии соответственно суммы постоянных и длительных нагрузок и всех нагрузок;

σ_s,crc. – см.п.4.13.

При отсутствии требований к конструкции по ограничению проницаемости и при выполнении условия

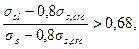(4.29)

можно проверять только продолжительное раскрытие трещин, а при невыполнении условия (4.29) - только непродолжительное раскрытие.

Для изгибаемых элементов в формулах (4.28а) и (4.29) значения σ_s,crc, σ_s и σ_sl можно заменить соответственно M_crc, M и M_l - момент от действия постоянных и длительных нагрузок.

Примеры расчета.

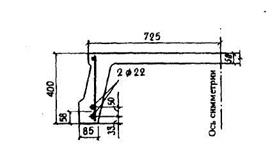
Пример 42. Дано:железобетонная плита перекрытия с размерами поперечного сечения (для половины сечения плиты) по черт.4.4; бетон класса В25 (R_bt,ser = 1,55 МПа, R_b,ser =18,5 МПа, Е_b = 30000 МПа); площадь сечения растянутой арматуры класса А400 А_s = 760 мм² (2Æ22); полный момент в середине пролета М = 69 кНм; все нагрузки постоянные и длительные.