Черт.3.51. К примеру расчета 41

1 - точка приложения сипы F; 2 - центр тяжести незамкнутого контура;3 - незамкнутый контур расчетного сечения

Требуется проверить плиту перекрытия на продавливание.

Расчет. Усредненную рабочую высоту плиты принимаем равной h_о =200 мм.

За сосредоточенную продавливающую силу F, направленной снизу вверх, принимаем нагрузку от перекрытия F = N = 150 кН; за площадь опирания этой силы - сечение колонны ахb = 500х400 мм.

Проверим прочность расчетного сечения незамкнутого контура. Размеры этого контура равны:

L_x = х_o + (a+h_o)/2 = 500 + (500 + 200) /2 = 850 мм;

L_y = b+h_o = 400 + 200 = 600 мм.

Периметр и момент инерции контура равны

и = 2L_x + L_y = 2·850 + 600 = 2300 мм;

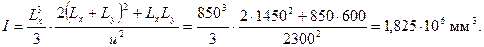
Эксцентриситет силы F

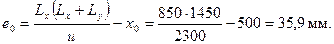
При принятых направлениях моментов М_suр и M_int (см. черт.3.51) наиболее напряженное волокно расчетного сечения расположено по краю сечения, наиболее удаленному от свободного края плиты. Это волокно расположено на расстоянии от центра тяжести равном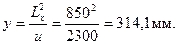

Тогда момент сопротивления равен:

W_b = I/у = 1,825·10⁶/314,1 = 581025мм².

Расчетный момент от колонн равен

М = M_loc/2= (М_suр + М_inf)/2=(80+90)/2=85 кНм.

Момент от эксцентричного приложения силы F равен F·e_o = 150·0,0359 = 5,4 кНм. Этот момент противоположен по знаку моменту M_loc, следовательно, М = 85 - 5,4 = 79,6 кНм. Проверяем прочность из условия (3.182)

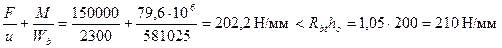
т.е. прочность сечения с незамкнутым контуром обеспечена.

Проверим прочность сечения замкнутого контура. Определяем его геометрические характеристики:

Периметр u = 2(a + b+ 2h_o) = 2(500+400+2·200) = 2600 мм;

Момент сопротивления

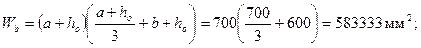
Момент равен М = М_loc /2 = 85 кНм.

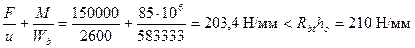
прочность плиты на продавливание обеспечена по всем сечениям.