контрастных структур
| a | b | c | d | e | f | g |
| 0.23 | 2.937 | 72,1 | 1.532 | 14,9 | ||
| k | l | m | n | X | Y | Z |
| 0.49 |
 а
а
 б
б
|  в
в
|
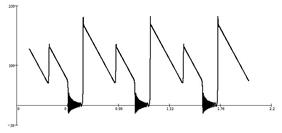
Рис.4. Проекция аттрактора (а, отмечены особые точки) с контрастными структурами и погранслоем (б)
Система (2) может иметь различное, в зависимости от числа действительных корней уравнения 4-й степени, количество особых точек. Это уравнение здесь не приводим ввиду его громоздкости.
В табл.3 представлены значения параметров модели и начальные условия, которые принимались при расчете.
Таблица 3
Параметры и начальные условия модели 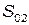
| a | b | c | d | e | f | g | h |
| 2,5 | 0,2 | 0,5 | 1,5 | ||||
| k | m | X | Y | Z | X0 | y0 | z0 |
| 0,5 |
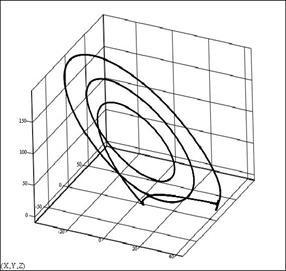
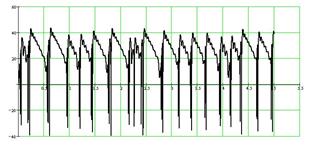
Практический интерес представляет решение системы, полученное при f = 8 (1/мин) и приведенное на рис.5. Здесь имеет место циклический характер работы системы. Временная зависимость переменных x и y показывает изменение числа автобусов и пассажиров на остановке, напоминающее известные функции из теории управления запасами, как и в модели (1). В течение некоторого времени число автобусов на остановке плавно уменьшается, число пассажиров остается до определенного момента почти постоянным, затем их количество заметно уменьшается и практически мгновенно (в масштабе времени одного цикла) осуществляется интенсивный переходный процесс, связанный с накоплением пассажиров и автобусов до исходного уровня. Эти пилообразные кривые представляют своего рода временные (контрастные, как и в модели грузового склада) структуры, показывающие согласованный характер работы всех элементов (остановок) макросистемы, т.е. самоорганизацию. Изучение подобных структур в реальных системах позволит сформулировать постановку задачи теории управления для создания требуемых типов временных структур в течение дня работы автобусного парка.
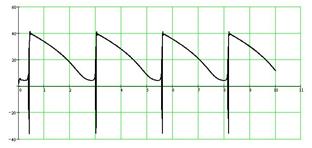
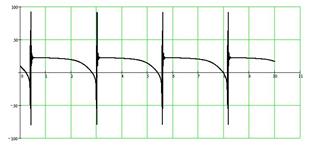
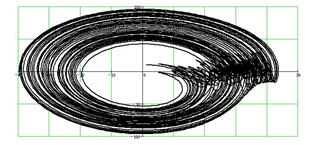
В модели реализуется каскад бифуркаций, приводящих к нерегулярному аттрактору. Параметры, приведенные в таблице, соответствуют этому решению, которое показано на рис.6. Таким образом, в системе уравнений (2) также имеется детерминированный хаос, возникающий в результате гомоклинического каскада бифуркаций [4].
| 
|
а б
Рис.5. Решение модели (2) при f = 8 (1/мин):
а – временные зависимости; б – фазовый портрет

| 
|
а б
Рис.6. Хаотический аттрактор в модели пассажирской остановки:
а – временные зависимости; б – проекции фазового портрета
Дата добавления: 2016-05-25; просмотров: 671;
