Изучение динамических моделей транспортных систем
Существует большое разнообразие подходов к описанию транспортных процессов и систем. Это обусловлено, с одной стороны, различием целей и задач, решаемых в конкретных ситуациях. С другой стороны, в любой транспортной системе (мы не касаемся специфики трубопроводного транспорта) можно выделить следующие основные элементы:
· транспортное средство;
· предприятие, осуществляющее грузовые и/или пассажирские перевозки;
· транспортная сеть;
· пункт погрузки-разгрузки;
· грузовой склад (терминал);
· пассажирский вокзал (пассажирская остановка);
· перевозочный (транспортный) процесс;
· поток транспортных средств и др.
Отличительными особенностями почти любой из перечисленных подсистем являются: наличие большого числа однородных элементов или элементов разной природы; дискретность состояний; наличие потоков случайных событий и случайных процессов. В качестве теоретических основ для моделирования перечисленных объектов применяются чаще всего аппараты теории линейного (нелинейного, динамического) программирования, массового обслуживания, управления запасами, игр и т.д. При этом делаются предположения либо о полностью детерминированном функционировании систем (например, в случае решения разнообразных транспортных задач линейного программирования), либо о вероятностном характере происходящих процессов (в большинстве других случаев) [1]. Подход, который используется в теории макросистем [2], позволяет расширить указанные рамки и допускает детерминированное поведение систем, состоящих из элементов со стохастическим типом поведения.
На рис.1 приведена схема транспортной макросистемы 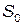 , где
, где 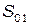 – грузовой склад;
– грузовой склад; 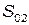 – пассажирская остановка;
– пассажирская остановка; 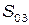 – участок улично-дорожной сети;
– участок улично-дорожной сети; 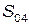 – гараж (парковка, автотранспортное предприятие и т.п.);
– гараж (парковка, автотранспортное предприятие и т.п.);  – грузоотправитель;
– грузоотправитель; 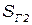 – грузополучатель;
– грузополучатель;  – место проживания пассажиров;
– место проживания пассажиров; 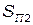 – место работы пассажиров и приобретения услуг.
– место работы пассажиров и приобретения услуг.
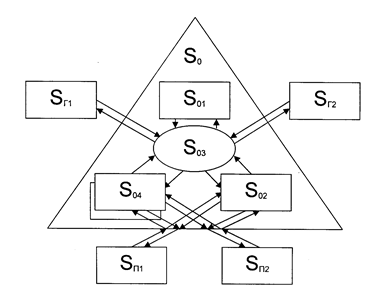
Рис.1. Схема транспортной макросистемы
Все перечисленные элементы также рассматриваются как макросистемы. Например, макросистема 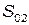 состоит из всех остановочных пунктов города. Каждый из них описывается собственными переменными, такими как число пассажиров, число автобусов, находящихся на остановке, число свободных мест в транспортном средстве (см. п.2.2). Складывая все переменные в один и тот же момент времени, которые являются случайными величинами, получаем описание системы в целом. Учитывая коллективный характер такого описания, можем предположить возникновение детерминированных связей, эффектов самоорганизации, синхронизации функционирования отдельных элементов и т.д. Аналогичное допущение действует и на подсистему
состоит из всех остановочных пунктов города. Каждый из них описывается собственными переменными, такими как число пассажиров, число автобусов, находящихся на остановке, число свободных мест в транспортном средстве (см. п.2.2). Складывая все переменные в один и тот же момент времени, которые являются случайными величинами, получаем описание системы в целом. Учитывая коллективный характер такого описания, можем предположить возникновение детерминированных связей, эффектов самоорганизации, синхронизации функционирования отдельных элементов и т.д. Аналогичное допущение действует и на подсистему 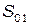 .
.
В макросистеме главным образом предполагается наличие потоков трех видов: пассажиров, грузов и транспортных средств. Можно установить достаточно большое количество цепочек, соединяющих узлы на рис.1 и соответствующих некоторым реальным перемещениям в транспортной системе. Каждый из потоков будет определяться собственной переменной, зависящей от времени. В результате могут быть сформулированы динамические модели вида:
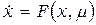
или
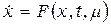 ,
,
где 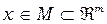 ,
,  ,
, 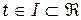 .
.
1.1. Модель грузового склада (макросистемы 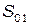 )
)
Данная модель может быть представлена в виде системы уравнений
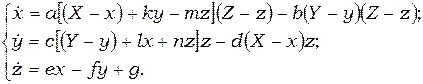 (1)
(1)
Переменные имеют следующий смысл: 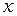 – автомобили, доставляющие груз;
– автомобили, доставляющие груз; 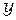 – автомобили, развозящие груз;
– автомобили, развозящие груз;  – количество груза на складе. Параметры в уравнениях (1) обозначают:
– количество груза на складе. Параметры в уравнениях (1) обозначают:  – число автомобилей, участвующих в доставке груза;
– число автомобилей, участвующих в доставке груза;  – число автомобилей, участвующих в развозе груза;
– число автомобилей, участвующих в развозе груза; 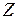 – предельная (или наиболее вероятная) емкость склада;
– предельная (или наиболее вероятная) емкость склада; 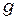 – интенсивность восполнения груза другими видами транспорта.
– интенсивность восполнения груза другими видами транспорта.
При формулировке настоящей модели, равно как и последующих, использовалось представление о балансе транспортных средств и груза (по аналогии с уравнением баланса массы в механике сплошной среды), а также учет основных причинно-следственных связей, приводящих к изменению поведения участников транспортной системы. Например, в первом уравнении учтено: чем больше груза на складе, тем больше автомобилей снимают с маршрута ( 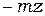 ); чем меньше запас z, тем интенсивнее будут поступать автомобили (Z – z); чем больше автомобилей стоит на погрузку, тем медленнее отбывают автомобили типа x (множитель Y – y); чем больше груза, тем сложнее разгрузиться (множитель Z – z) и т.д. Отсюда становится ясным смысл коэффициентов
); чем меньше запас z, тем интенсивнее будут поступать автомобили (Z – z); чем больше автомобилей стоит на погрузку, тем медленнее отбывают автомобили типа x (множитель Y – y); чем больше груза, тем сложнее разгрузиться (множитель Z – z) и т.д. Отсюда становится ясным смысл коэффициентов 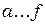 , которые выражают интенсивность прироста или убывания переменных в результате действия соответствующих причин.
, которые выражают интенсивность прироста или убывания переменных в результате действия соответствующих причин.
1.2. Модель пассажирской остановки (макросистемы 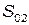 )
)
Модель может быть сформулирована в виде системы [3]:
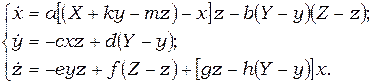 (2)
(2)
Здесь переменными являются: х – количество автобусов, находящихся на остановке; у – количество пассажиров, ожидающих посадку; z – число свободных мест в автобусах, находящихся на остановке. Остальные параметры имеют следующий смысл: Х – среднее (нормативное) число автобусов, работающих на маршруте; Y – среднее количество пассажиров на остановке (условная «вместимость» остановки); Z – среднее число мест для пассажиров (вместимость автобуса). Коэффициенты модели характеризуют: а – интенсивность прибытия автобусов на остановку (имеет размерность 1/(мест·мин)); b – интенсивность отправления автобусов от остановки (авт/(пасс·мест·мин)); с – интенсивность посадки пассажиров в автобусы (пасс/авт·мест·мин)); d – интенсивность прибытия пассажиров на остановку (1/мин); е – скорость уменьшения числа свободных мест вследствие посадки пассажиров (1/(пасс·мин)); f – интенсивность увеличения числа свободных мест за счет высадки пассажиров (1/мин); g – скорость роста числа свободных мест, «прибывающих» вместе с автобусами (1/авт·мин));
h – интенсивность «убывания» свободных мест, не занятых пассажирами до отправления автобуса (1/пасс·авт·мин)); k – интенсивность выхода на линию автобусов сверх нормативного значения при увеличении числа пассажиров на остановках (авт/пасс); m – интенсивность «схода» автобусов с маршрутов вследствие роста числа свободных мест (авт/мест).
Слагаемые в правых частях уравнений имеют следующий смысл. В первом уравнении (4) слагаемое с знаком «+» отражает поступление автобусов на остановку, зависящее от разности общего количества автобусов, находящихся на маршрутах, и числа автобусов на остановке. В этом слагаемом учитываются также выпуск автобусов на маршрут при росте числа пассажиров на остановке (например, в часы «пик»), а также «сход» с маршрута при увеличении числа свободных мест в автобусе. Это слагаемое пропорционально количеству свободных мест в автобусах на остановке (чем больше свободных мест, тем интенсивнее будут автобусы поступать на посадку с целью загрузки – или сходят с маршрута, о чем уже сказано). Слагаемое со знаком «–» отражает процесс отправления автобуса от остановки. Оно осуществляется быстрее, если, с одной стороны, на остановке мало пассажиров (становится короче по времени процесс посадки) или, с другой стороны, если мало свободных мест в самом автобусе (пассажиры отказываются от посадки). Таким образом, имеем произведение  .
.
Во втором уравнении слагаемое со знаком «+» описывает приход пассажиров на остановку: чем меньше занята остановка, тем выше вероятность увеличения числа пассажиров. Чем больше занята остановка (уменьшение разности  ), тем больше пассажиров будет ее покидать с целью поиска альтернативного способа передвижения. Чем больше пассажиров уже находится на остановке, тем меньше потенциальных пассажиров находится за ее пределами. Слагаемое со знаком «–» описывает процесс посадки пассажиров в автобусы: чем больше автобусов на остановке и чем больше на ней свободных мест, тем выше вероятность посадки.
), тем больше пассажиров будет ее покидать с целью поиска альтернативного способа передвижения. Чем больше пассажиров уже находится на остановке, тем меньше потенциальных пассажиров находится за ее пределами. Слагаемое со знаком «–» описывает процесс посадки пассажиров в автобусы: чем больше автобусов на остановке и чем больше на ней свободных мест, тем выше вероятность посадки.
В третьем уравнении слагаемое  учитывает процесс увеличения числа свободных мест за счет высадки пассажиров (чем больше пассажиров в автобусе, тем вероятнее выход пассажиров на остановке). Второе слагаемое со знаком «+» учитывает «поступление» свободных мест с автобусами. Слагаемое со знаком «–» описывает процесс уменьшения свободных мест за счет посадки пассажиров. Это слагаемое пропорционально произведению yz: чем больше пассажиров на остановке и чем больше свободных мест, тем выше вероятность того, что свободные места будут заняты.
учитывает процесс увеличения числа свободных мест за счет высадки пассажиров (чем больше пассажиров в автобусе, тем вероятнее выход пассажиров на остановке). Второе слагаемое со знаком «+» учитывает «поступление» свободных мест с автобусами. Слагаемое со знаком «–» описывает процесс уменьшения свободных мест за счет посадки пассажиров. Это слагаемое пропорционально произведению yz: чем больше пассажиров на остановке и чем больше свободных мест, тем выше вероятность того, что свободные места будут заняты.
Анализ описанных выше моделей (1) и (2) выполняется при допущении, что все параметры и коэффициенты положительны (некоторые в частных случаях принимаются равными нулю) и не зависят от времени. Исследование систем уравнений начинаем с определения точек стационарных состояний, их типа и устойчивости. Модель (1) в общем случае имеет три особые точки, координаты которых определяются формулами:
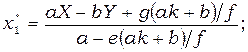
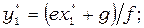
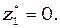 (3)
(3)
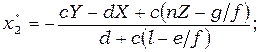
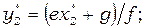
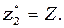 (4)
(4)
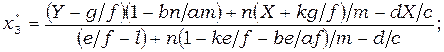
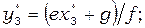
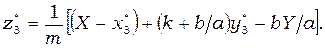 (5)
(5)
В частном случае, при  , в системе могут быть две особые точки. Тип и устойчивость точек определяется, как обычно, характеристическим уравнением для линеаризованной в окрестности этих точек системы.
, в системе могут быть две особые точки. Тип и устойчивость точек определяется, как обычно, характеристическим уравнением для линеаризованной в окрестности этих точек системы.
Система (1) диссипативна при условии:
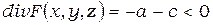 ,
,
которое выполняется всегда при положительных а и с. Следовательно, имеется предположение о возможности существования гетероклинических контуров, определяющих вид траекторий в фазовом пространстве.
Уравнения (1) и (2) исследовались численно методом Рунге-Кутта с переменным шагом и точностью 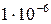 .
.
Зафиксируем константы модели (1), как указано в табл.1. Рассматривая коэффициенты d, e, f, k, l, m, n в качестве бифуркационных параметров, можем обнаружить все основные виды решений, характерных для трехмерных автономных нелинейных систем: стационарное состояние, предельный цикл, хаотический аттрактор и другие типы циклов различной периодичности. Например, на рис.2 и 3 представлены хаотический аттрактор, а также циклы типа  и
и 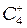 (в терминологии, принятой в работе [4]).
(в терминологии, принятой в работе [4]).
Таблица 1
Параметры модели макросистемы 
| a | b | c | d | e | f | g |
| 0.2 | 2.5 | 0.3 | 1.535 | |||
| k | l | m | n | X | Y | Z |
 а
а
 б
б
|  в
в
|
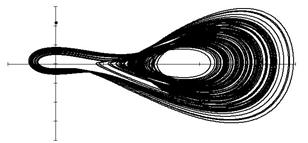
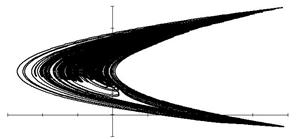
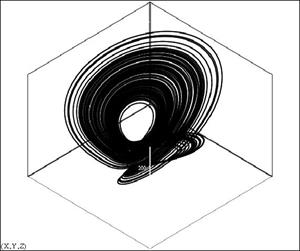
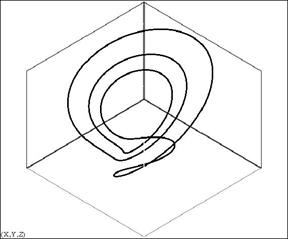
Рис.2. Проекции хаотического аттрактора (параметры соответствуют табл.1)
в координатах: а – z(y); б – x(z)
| 
|
а б
Рис.3. Циклы типа 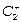 и
и 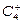 при d = 2, e = 0.5, k = m = 0.5, l = n = 1
при d = 2, e = 0.5, k = m = 0.5, l = n = 1
(остальные параметры как в табл.1): а – f = 21; б – f = 10
Предположение о возможности существования гетероклинического контура косвенно подтверждается видом аттрактора (рис.4), полученного в системе (1) с параметрами, заданными в табл.2. На рис.4, б приведена зависимость z(t), которая свидетельствует о существовании так называемых контрастных структур и пограничного слоя [5] в решениях модели. Эти особенности являются неслучайными, так как при заданных в табл.2 параметрах система стремится к сингулярно возмущенной задаче, что и является, по-видимому, источником подобных эффектов. Зависимость z(t) весьма напоминает при этом некоторую стратегию управления запасами, что придает модели (1) практическую привлекательность.
Таблица 2
Дата добавления: 2016-05-25; просмотров: 1269;
