Исследование замкнутой одноканальной СМО

СМО, изученные в предыдущей лабораторной работе, обладали общим свойством – входящий поток заявок П_вх и его интенсивность не зависели от состояний системы, источник поступающих заявок находился вне системы. Рассмотрим СМО, в которых интенсивность потока поступающих заявок зависит от состояния системы. Такие СМО называют замкнутыми или системами Энгсета по имени Т. Энгсета, который впервые дал их полный анализ.

Пусть одноканальная СМО содержит i источников заявок, каждый из которых порождает простейший поток заявок с интенсивностью λ.

Заявка, пришедшая от источника в момент, когда канал занят, становится в очередь и ждет обслуживания. При этом источник может подать следующую заявку только в том случае, если поданная им предыдущая заявка уже обслужена. Среднее время обслуживания каналом одной заявки (безразлично из каких источников)

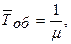
где μ – интенсивность простейшего потока обслуживании.

Таким образом, имеем своеобразную СМО, содержащую конечное число источников заявок, каждый из которых может находиться в одном из двух состояний: активном или пассивном. Активное состояние источника – это такое состояние, при котором уже обслужена поданная им последняя заявка. Пассивное состояние характеризуется тем, что поданная источником последняя заявка еще не обслужена, т.е. либо стоит в очереди, либо находится под обслуживанием.

В активном состоянии источник может подавать заявки, а в пассивном – нет. Следовательно, интенсивность общего потока заявок зависит от того, сколько источников находится в пассивном состоянии, т.е. сколько заявок связано с процессом обслуживания (стоит в очереди или непосредственно обслуживается).

Характерным для замкнутой СМО является зависимость потока заявок от состояний самой СМО. Эта зависимость проявляется существенно при конечном небольшом числе источников заявок. Но если число источников достаточно велико, то практически можно считать, что интенсивность потока заявок не зависит от состояний СМО.

Занумеруем состояния СМО по числу источников, находящихся в пассивном состоянии, т.е. по числу заявок, находящихся в очереди и под обслуживанием:

S₀ – все i источников находятся в активном состоянии,

канал свободен, очереди нет;

S₁ – один источник находится в пассивном состоянии, канал обслуживает поданную этим источником заявку, очереди нет;

S₂ – два источника находятся в пассивном состоянии, заявка, поданная одним из них, обслуживается, а заявка, поданная другим источником, стоит в очереди;

S_i –все i источников находятся в пассивном состоянии, заявка, поданная одним из них, обслуживается, а i–1 заявок, поданных остальными источниками, стоят в очереди.

Граф состояний приведен на рис.1.

Из состояния S₀в состояние S₁ систему переводит суммарный поток, слагающийся из потоков всех i активных источников; поэтому интенсивность этого суммарного потока λ₀₁ = iλ. Из состояния S₁ в состояние S₂система переходит под воздействием суммарного потока уже i–1 потоков активных источников, поскольку один источник находится в пассивном состоянии; следовательно, λ₁₂= (i–1)λ и т.д. Из состояния S_i-1в состояние S_i систему переводит только один поток, порождаемый единственным источником, находящимся в активном состоянии (все остальные i–1 источников в пассивном состоянии); поэтому λ_i-1,_i= λ. Таким образом, мы нашли все плотности вероятностей переходов системы по стрелкам слева направо. Интенсивности же потоков, переводящих СМО по стрелкам справа налево, все одинаковы и равны μ, поскольку все время работает один канал с интенсивностью обслуживания μ. Таким образом, λ_k,k-1=μ, k=1,…,i.

Как видно из структуры графа состояний данной СМО (рис.1), в ней протекает процесс гибели и размножения. Тогда для определения предельных вероятностей состояний получим:

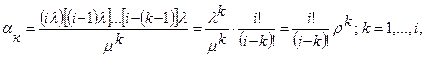
где 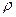= λ/μ – показатель нагрузки системы, порождаемой каждым источником заявок.

Найдем вероятности состояний:

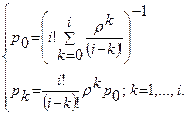
Событие, состоящее в том, что канал занят, и событие, состоящее в том, что канал свободен, противоположны и потому вероятности этих событий в сумме дают единицу. Следовательно, вероятность того, что канал занят

р_зан = 1 – р₀,

где р₀ –вероятность того, что канал свободен. Так как производительность канала – μ заявок в единицу времени, то абсолютная пропускная способность СМО

А = р_зан μ = (1 – р₀) μ.

Напомним, что интенсивность ν выходящего потока П_вых обслуженных заявок совпадает с абсолютной пропускной способностью А:

ν = А = (1 – р₀) μ.

Так как каждая заявка рано или поздно будет обслужена каналом, то относительная пропускная способность СМО равна единице Q = 1.

Вычислим среднее число 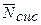заявок, находящихся в системе, т.е. в очереди и под обслуживанием, иными словами, среднее число 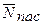источников, находящихся в пассивном состоянии.

В рассматриваемой СМО всего i источников заявок, из которых в среднем 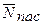находятся в пассивном состоянии. Следовательно, i – 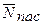источников находятся в активном состоянии и каждый из них порождает поток заявок с интенсивностью λ. Тогда средний суммарный входящий поток (порождаемый активными источниками) будет иметь среднюю интенсивность заявок в единицу времени:

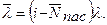(1)

Поскольку все эти заявки обслуживаются каналом, то

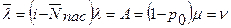(2)

Формула (2) показывает, что средняя интенсивность 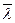входящего потока равна интенсивности ν выходящего потока.

Из формулы (2)

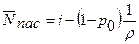. (3)