Примеры решения задач. 5.2.1 Четырехполюсник, схема соединения элементов которого приведена на рис
5.2.1 Четырехполюсник, схема соединения элементов которого приведена на рис. 5.13, имеет параметры R=XL=10 Ом, ХС=20 Ом.
 Определить коэффициенты А-формы записи уравнений четырехполюсника и убедиться, что результаты удовлетворяют соотношению AD-BC=1.
Определить коэффициенты А-формы записи уравнений четырехполюсника и убедиться, что результаты удовлетворяют соотношению AD-BC=1.
Расчет коэффициентов выполнить с помощью законов Кирхгофа и по входным сопротивлениям в режиме холостого хода и короткого замыкания.
Уравнения четырехполюсника в А-форме имеют вид:
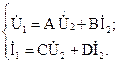
1) Составим уравнения по законам Кирхгофа для рассматриваемой схемы.
Согласно первому закону Кирхгофа: 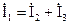 .
.
По второму закону Кирхгофа составим уравнения для внешнего и правого контуров схемы:
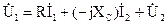 ;
;
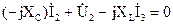 .
.
Из второго уравнения выразим ток:
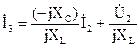 ,
,
и подставим полученное выражение в уравнение, составленное по первому закону Кирхгофа:
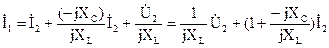 .
.
Сравнив полученное выражение с уравнением четырехполюсника, составленным для тока, можно определить коэффициенты 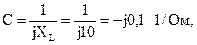 и
и
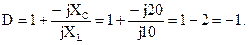
Для определения коэффициентов А и В подставим выражение, полученное для тока 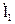 в уравнение, составленное по второму закону Кирхгофа для внешнего контура:
в уравнение, составленное по второму закону Кирхгофа для внешнего контура:
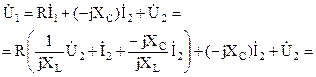
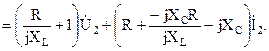
Сравнив полученное выражение с уравнением четырехполюсника, составленным относительно напряжения, найдем коэффициенты:
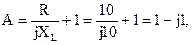
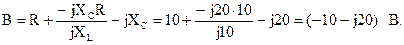
Проверим выполнение соотношения между коэффициентами А-формы записи уравнений четырехполюсника:
AD – BC = (1 – j1)(–1) – (–10 – j20)(–j0,1) = –1 + j1 – j1+ 2 = 1,
что и требовалось доказать.
2) Рассчитаем коэффициенты по входным сопротивлениям в режиме холостого хода и короткого замыкания.
Рассчитаем входные сопротивления в режимах холостого хода и короткого замыкания при прямом включении четырехполюсника (рис.2.14, а, б):
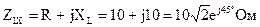 ,
,
 |
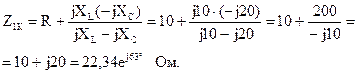
Рассчитаем входные сопротивления в режимах холостого хода и короткого замыкания при обратном включении четырехполюсника (рис. 5.15, а, б):
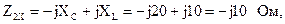
 |
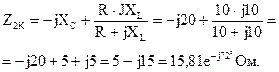
По известным формулам рассчитаем значения коэффициентов:
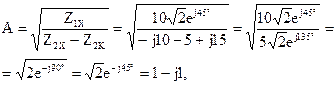
B=A Z2K=(1-j1)·(5-j15)=5-j5-j15-15= (-10-j20) Ом;
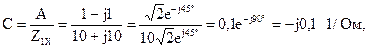
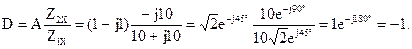
Результаты расчетов соответствуют значениям коэффициентов, полученным с помощью законов Кирхгофа.
 5.2.2Четырехполюсник, схема которого приведена на рис. 5.16, имеет параметры:
5.2.2Четырехполюсник, схема которого приведена на рис. 5.16, имеет параметры:
R = XL = 10 Ом, ХС = 20 Ом. Определить коэффициенты А-формы записи уравнений четырехполюсника и убедиться, что результаты удовлетворяют соотношению AD – BC = 1.
Расчет коэффициентов выполнить с помощью законов Кирхгофа и по входным сопротивлениям в режиме холостого хода и короткого замыкания.
Уравнения четырехполюсника в А-форме имеют вид:
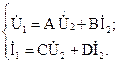
1) Составим уравнения по законам Кирхгофа для рассматриваемой схемы.
По первому закону Кирхгофа составим два уравнения
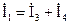 и
и 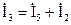
По второму закону Кирхгофа составим уравнение для внешнего контура схемы:
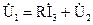
Так как напряжение на зажимах четвертой ветви рано входному напряжению четырехполюсника, а напряжение на пятой ветви равно – выходному, то по закону Ома можно выразить токи в ветвях:
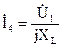 и
и 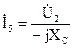 .
.
Выразим значение тока третьей ветви через выходные режимные параметры четырехполюсника, подставив выражение для тока 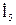 в уравнение, составленное по первому закону Кирхгофа
в уравнение, составленное по первому закону Кирхгофа 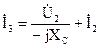 . Полученное выражение подставим в уравнение, составленное по второму закону Кирхгофа:
. Полученное выражение подставим в уравнение, составленное по второму закону Кирхгофа:
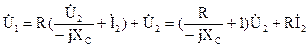 .
.
Сравнив полученное выражение с уравнением четырехполюсника, составленным относительно напряжения, найдем коэффициенты:
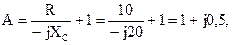
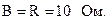
Можно записать, подставив одно в другое уравнения, составленные по первому закону Кирхгофа  .
.
Подставим в полученное уравнение значения токов четвертой и пятой ветвей и уже известное выражение для входного напряжения:
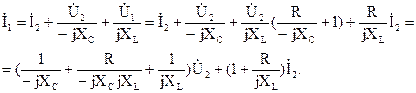
Сравнив полученное выражение с уравнением четырехполюсника, составленным относительно входного тока, найдем коэффициенты:
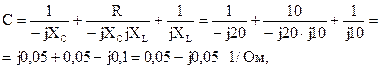
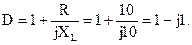
Проверим выполнение соотношения между коэффициентами А-формы записи уравнений четырехполюсника:
AD-BC=(1+j0,5)·(1-j1)-10·(0,05-j0,05)=1-j1+j0,5+0,5-0,5+j0,5=1.
2) Рассчитаем коэффициенты по входным сопротивлениям в режиме холостого хода и короткого замыкания.
 |
Рассчитаем входные сопротивления в режимах холостого хода и короткого замыкания при прямом включении четырехполюсника (рис. 5.17, а и б).
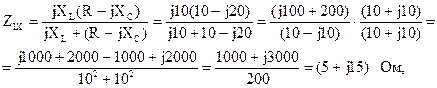
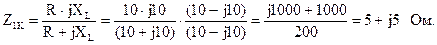
Рассчитаем входные сопротивления в режимах холостого хода и короткого замыкания при обратном включении четырехполюсника (рис. 5.18, а и б).
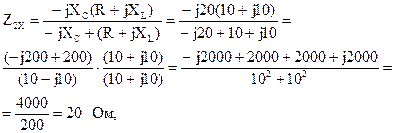
 |
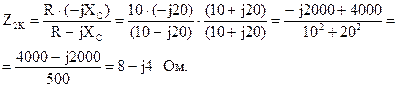
По известным формулам рассчитаем значения коэффициентов уравнений А-формы записи:
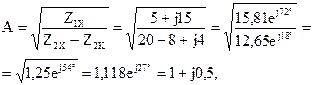
B = A Z2K = (1 + j0,5)·(8 – j4) = 8 + j4 – j4 + 2 = 10 Ом;
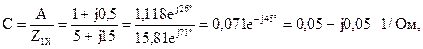
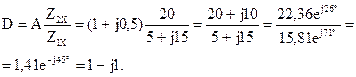
Результаты расчетов соответствуют значениям коэффициентов, полученным с помощью законов Кирхгофа.
5.2.3 Несимметричный четырехполюсник имеет параметры А = 1; В = 2,83еj45° Ом; С = j0,5 См; D = j1. Найти характеристические сопротивления четырехполюсника и постоянную передачи.
Найдем характеристические сопротивления:
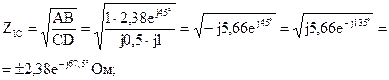
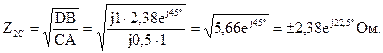
Отрицательные значения комплексного сопротивления не имеют физического смысла, так как они не реализуемы.
Определим постоянную передачи:
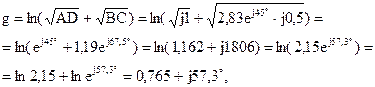
где коэффициент затухания 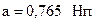 , а коэффициент фазы
, а коэффициент фазы 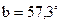 или
или 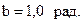
 5.2.4 Для четырехполюсника, эквивалентная схема которого приведена на рис. 5.19, составить уравнения, выражающие зависимость комплексных напряжения
5.2.4 Для четырехполюсника, эквивалентная схема которого приведена на рис. 5.19, составить уравнения, выражающие зависимость комплексных напряжения 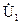 входной ветви и тока
входной ветви и тока 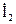 выходной ветви от комплексных тока
выходной ветви от комплексных тока 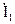 входной ветви и напряжения
входной ветви и напряжения 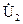 выходной ветви.
выходной ветви.
Параметры элементов цепи: Z0=12 Ом, Z2=6 Ом, Z1=(4+j3) Ом.
Искомую зависимость выражают уравнения четырехполюсника Н-типа:
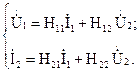
Коэффициенты Н11, Н12, Н21 и Н22 можно определить на основе рассмотрения исходной схемы сначала при разомкнутых первичных зажимах, а затем при короткозамкнутых вторичных полюсах с одновременным анализом уравнений Н-формы записи, соответствующим этим состояниям.
При разомкнутых первичных зажимах 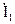 = 0 и система уравнений примет вид:
= 0 и система уравнений примет вид:
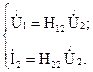 откуда запишем
откуда запишем 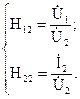
Для рассматриваемого режима:
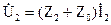 ,
, 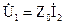 ,
,
и тогда можно определить коэффициенты:
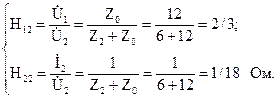
При короткозамкнутых вторичных полюсах 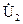 =0 система уравнений примет вид:
=0 система уравнений примет вид:
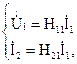 откуда запишем
откуда запишем 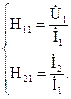
Для рассматриваемого режима:
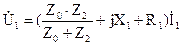 ,
, 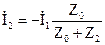 .
.
Тогда можно определить коэффициенты:
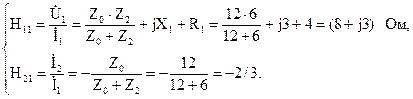
5.2.5 Выразить Z параметры взаимного четырехполюсника через сопротивления его Т-схемы замещения (рис. 5.20).
 Система уравнений четырехполюсника в Z-форме записи имеет вид:
Система уравнений четырехполюсника в Z-форме записи имеет вид:
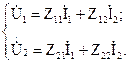
Запишем уравнения по законам Кирхгофа, связывающие напряжения четырехполюсника с входным и выходным токами, одновременно проводя анализ уравнений z-формы:
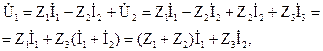
где 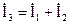 – ток в поперечной ветви;
– ток в поперечной ветви; 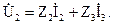
Сравнив выражение, полученное для входного напряжения четырехполюсника с первым уравнением Z- формы, можно определить коэффициенты:
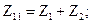
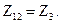
Относительно выходного напряжения запишем:
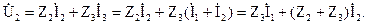
Сравнив полученное уравнение со вторым уравнением системы уравнений в z-форме, определим коэффициенты:
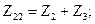
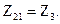
Из полученных значений видно, что для взаимного четырехполюсника равны коэффициенты
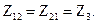
5.2.6 При питании четырехполюсника со стороны первичных зажимов были измерены U1, I1, P1 в двух режимах:
а) холостого хода U1X = 100 B; I1X = 1 A; P1X = 0; б) в режиме короткого замыкания U1К = 100 B; I1К = 1,41 A; P1К = 100 Вт. В обоих случаях характер сопротивлений емкостный.
При обратном включении четырехполюсника при закороченных первичных зажимах были измерены U2К = 100 B; I2К = 1 A; P2К = 100 Вт. Известно, что Z1K/Z2K = Z1X/Z2X. Рассчитать сопротивления прямого, обратного холостого хода и короткого замыкания. Определить по ним Z-параметры четырехполюсника.
При прямом включении четырехполюсника входные сопротивления для режимов холостого хода и короткого замыкания по показаниям измерительных приборов определяются:
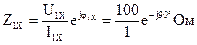 ,
,
где 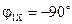 так как, согласно исходным данным, нагрузка носит чисто емкостный характер (Р1Х=0);
так как, согласно исходным данным, нагрузка носит чисто емкостный характер (Р1Х=0);
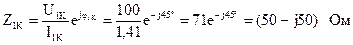 ,
,
где 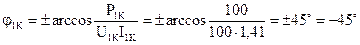 ,
,
так как известно, что характер сопротивлений емкостный.
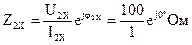 ,
,
где 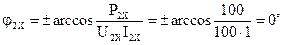 .
.
Сопротивление Z2K найдем из соотношения Z1K/Z2K = Z1X/Z2X:
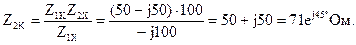
Уравнения четырехполюсника в Z-форме записи имеют вид:
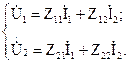
Для режима холостого хода при прямом 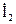 = 0 и обратном
= 0 и обратном 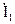 = 0 включении четырехполюсника запишем:
= 0 включении четырехполюсника запишем:
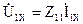 тогда
тогда 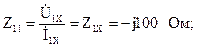
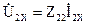 тогда
тогда 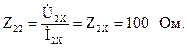
Для режима короткого замыкания на вторичных зажимах четырехполюсника ( 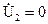 ) запишем:
) запишем:
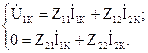
Выразим из второго уравнения ток на выходе четырехполюсника, и подставим полученное выражение в первое уравнение:
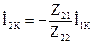 , тогда
, тогда 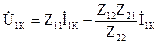 .
.
Сопротивление короткого замыкания со стороны первичных зажимов:
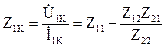 .
.
Отсюда рассчитаем коэффициенты:
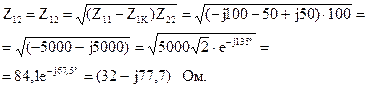
 5.2.7 Для симметричного четырехполюсника, работающего в режиме холостого хода, на рис. 5.21 задана векторная диаграмма токов и напряжений. Определить А-параметры четырехполюсника. Действующие значения тока и напряжений: U1Х = 100 В; U2Х = 200 В; I1Х = 2,5 А.
5.2.7 Для симметричного четырехполюсника, работающего в режиме холостого хода, на рис. 5.21 задана векторная диаграмма токов и напряжений. Определить А-параметры четырехполюсника. Действующие значения тока и напряжений: U1Х = 100 В; U2Х = 200 В; I1Х = 2,5 А.


 Запишем уравнения четырехполюсника А-формы для режима холостого хода (
Запишем уравнения четырехполюсника А-формы для режима холостого хода ( 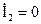 ):
):
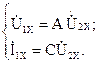
Действующие значения тока и напряжений на зажимах четырехполюсника в режиме холостого хода заданы, а их начальные фазы можно определить по векторной диаграмме. Тогда уравнения четырехполюсника запишутся, как
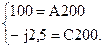
Отсюда коэффициенты А = 0,5, С = –j0,0125 1/Ом.
Для симметричного четырехполюсника D = A = 0,5.
Из соотношения, связывающего коэффициенты А-формы AD – BC = 1 определим коэффициент В:
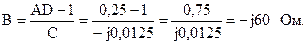
5.2.8 Для ослабления сигнала в нагрузке между нагрузкой и источником питания включен симметричный четырехполюсник. Вычислить параметры Т-схемы замещения, если он нагружен на согласованное сопротивление ZH = ZC = 200 Ом, а сигнал нужно ослабить на 0,5 Нп без его задержки во времени.
Параметры Т-схемы замещения легко получить через значения коэффициентов А-формы записи уравнений:
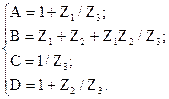 тогда
тогда 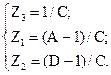
Определим коэффициенты А-формы, составив уравнения:
A = D, так как четырехполюсник симметричный;
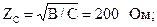
е(a+jb) = 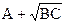 =e0,5, так как сигнал передается без задержки во времени, то коэффициент фазы b = 0; A2 – BC = 1.
=e0,5, так как сигнал передается без задержки во времени, то коэффициент фазы b = 0; A2 – BC = 1.
Составим систему уравнений с тремя неизвестными коэффициентами:
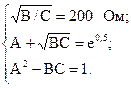
Решаем систему уравнений и находим коэффициенты:
А = 1,128; C = 0,0026 1/Ом; B = 10,2 Ом.
По рассчитанным значениям коэффициентов определим параметры симметричной Т-схемы замещения:
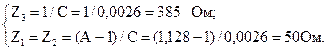
Как видно по значениям полученных комплексных сопротивлений схема рассматриваемого четырехполюсника реализована на активных сопротивлениях.
5.2.9 Определить параметры П-схемы замещения симметричного четырехполюсника, нагруженного на характеристическое сопротивление ZH = ZC = 500 Ом, с помощью которого осуществляется задержка синусоидального сигнала на четверть периода без его ослабления.
Параметры П-схемы замещения легко получить через значения коэффициентов А-формы записи уравнений:
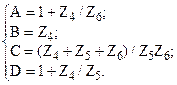 откуда
откуда 
Определим коэффициенты А-формы, составив уравнения:
A = D, так как четырехполюсник симметричный;
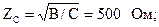
е(a+jb) = 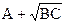 =ej90°, так как сигнал передается без ослабления, то коэффициент затухания a = 0; так как задержка во времени составляет четверть периода, то коэффициент фазы b=90°; A2 – BC = 1.
=ej90°, так как сигнал передается без ослабления, то коэффициент затухания a = 0; так как задержка во времени составляет четверть периода, то коэффициент фазы b=90°; A2 – BC = 1.
Составим систему уравнений:
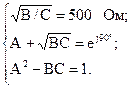
Решив эту систему уравнений найдем значения коэффициентов А = 0; В = j500 Ом; С = j0,002 1/Ом.
По рассчитанным значениям коэффициентов определим параметры симметричной П-схемы замещения:
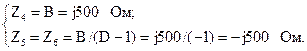
Как видно по значениям полученных комплексных сопротивлений схема рассматриваемого четырехполюсника реализована полностью на чисто реактивных элементах. В последовательной ветви включена идеальная индуктивная катушка, а в продольных ветвях конденсаторы.
5.2.10Определить параметры полосового фильтра, имеющего Т-образную схему (рис. 5.22), нагруженного на характеристическое сопротивление 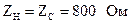 при резонансной частоте. Нижняя граница полосы пропускания f1 = 750 Гц, верхняя граница полосы пропускания f2 = 850 Гц.
при резонансной частоте. Нижняя граница полосы пропускания f1 = 750 Гц, верхняя граница полосы пропускания f2 = 850 Гц.


Резонансная частота 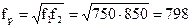 Гц.
Гц.
Параметры Т-образной схемы:
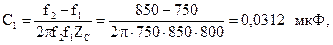
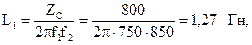
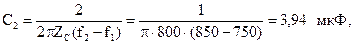
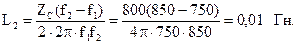
Дата добавления: 2016-05-25; просмотров: 11888;
