Соединенными резистором и индуктивной катушкой

Пусть цепь, показанная на рис. 6.1, включается на постоянное напряжение U.

В электротехнической практике это может быть подключение к источнику постоянного напряжения электромагнитов, реле, электрических машин постоянного тока и других электромагнитных устройств. После коммутации в цепи возникает переходный процесс, во время которого все электрические величины будут изменяться до своего установившегося значения.

Уравнение электрического состояния цепи (рис. 6.1) после замыкания ключа, записанное относительно тока:

.

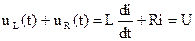Решение этого уравнения находится в виде суммы общего решения однородного (свободная составляющая) и частного решения неоднородного (принужденная составляющая) уравнений: i(t) = i_св(t) + i_пр.

Для определения принужденного значения искомого тока необходимо рассчитать ток цепи в установившемся послекоммутационном режиме. Применительно к рассматриваемой цепи принужденный ток определяется как i_пр = U/R, так как индуктивное сопротивление катушки постоянному току равно нулю.

Для определения свободной составляющей необходимо найти корни характеристического уравнения, которое получается путем замены в однородном дифференциальном уравнении первой производной тока на р, а самой функции тока на р⁰, то есть на единицу:

pL+R = 0, тогда p = -R/L.

Характеристическое уравнение имеет один корень, поэтому свободная составляющая будет состоять из одного слагаемого и выражение для переходного тока можно записать:

i(t)=Ae^pt +U/R= .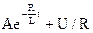

Для определения постоянной интегрирования А рассмотрим искомую функцию в момент времени t = 0: i(0+) = A+U/R.

В докоммутационной схеме ток индуктивности был равен нулю, так как цепь была отключена от источника энергии. Тогда согласно первому закону коммутации:

i(0+) = i_L(0+) = i_L(0–) = 0,

и постоянная интегрирования может быть определена из уравнения 0 = A + U/R, откуда А = –U/R.

Искомая функция переходного тока будет иметь вид:

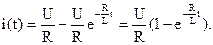
Напряжение на резистивном элементе цепи с сопротивлением R можно найти по закону Ома:

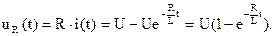
Напряжение на индуктивном элементе находится:

.

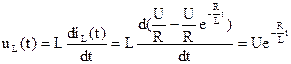Кривые изменения переходных токов и напряжений показаны на рис. 6.2 и 6.3 соответственно.

Свободную составляющую тока удобно представлять в виде: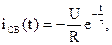

где τ = 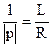имеет размерность времени и называется постоянной времени переходного процесса. Постоянная времени имеет физический и геометрический смысл.

Физический смысл постоянной времени τ: это время, в течение которого свободная составляющая, затухая, уменьшается в е раз по сравнению со своим предыдущим значением.

Например,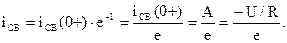

Геометрический смысл постоянной времени τ: постоянная времени численно равна длине любой подкасательной (рис. 6.2). Для графического определения τ проводится касательная к кривой свободной составляющей любой электрической величины в любой точке, и на оси времени находится подка
сательная.

Рис. 6.2 Рис. 6.3

Переходный процесс можно считать практически завершенным через промежуток времени t = 4÷5τ, а теоретически он длится бесконечно долго, так как экспонента свободной составляющей никогда не пересечет ось времени.