Классическим методом
Переходные функции тока и напряжения имеют вид:
i(t) = iсв(t) + iпр, u(t) = uсв(t) + uпр.
При расчете переходных процессов классическим методом удобно использовать следующий алгоритм.
1 Показать положительные направления токов и напряжений на элементах рассматриваемой цепи. В дальнейшем выбранные направления должны оставаться неизменными.
2 Определить независимые начальные значения, используя законы коммутации iL(0+) = iL(0–) и uC(0+) = uC(0–). Для этого необходимо рассчитать ток индуктивной катушки iL(0–) и напряжение на конденсаторе uC(0-) в цепи до коммутации.
3 Рассчитать принужденную составляющую искомой величины. Для этого необходимо определить установившиеся значения токов и напряжений в послекоммутационном режиме. Необходимо помнить, что в цепях постоянного тока в установившемся режиме индуктивная катушка представляет собой проводник с сопротивлением равным нулю, а конденсатор – разомкнутый участок цепи.
4 Составить характеристическое уравнение и найти его корни. Для этого необходимо определить входное сопротивление Z(p) относительно любых разомкнутых зажимов пассивной части схемы после коммутации, в которой все источники электрической энергии исключены, а реактивные индуктивные и емкостные сопротивления заменены на операторные сопротивления Lp и 1/Cp. Полученное выражение приравнивается к нулю и находятся его корни.
5 Рассчитать свободную составляющую
iсв(t)= 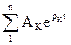 или uсв(t) =
или uсв(t) = 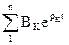 , то есть определить постоянные интегрирования АК и ВК. Для этого необходимо рассмотреть искомую функцию в момент времени t = 0+ и, используя известные значения независимых и зависимых начальных условий, определить постоянные интегрирования.
, то есть определить постоянные интегрирования АК и ВК. Для этого необходимо рассмотреть искомую функцию в момент времени t = 0+ и, используя известные значения независимых и зависимых начальных условий, определить постоянные интегрирования.
6 Построить график временной зависимости искомой функции на промежутке времени t = 0 ÷ 5τ.
При расчете переходных процессов классическим методом необходимо иметь в виду, что проще всего вести расчет тех переходных функций, начальные значения которых определяются законами коммутации, то есть тока индуктивной катушки iL(t) и напряжения конденсатора uC(t). Остальные переходные функции удобно находить с помощью законов Ома и Кирхгофа, записанных в дифференциальной форме.
Дата добавления: 2016-05-25; просмотров: 706;
