Соединением резистора и конденсатора

Рассмотрим переходный процесс при включении цепи R, C на постоянное напряжение (рис. 6.4). После замыкания ключа в цепи возникает ток и конденсатор заряжается до величины напряжения источника U, после чего ток становится равным нулю. Это физическое понимание переходного процесса. Опишем теперь этот процесс математически.

В соответствии со вторым законом Кирхгофа составим уравнение электрического состояния для рассматриваемой цепи относительно напряжения конденсатора:

.

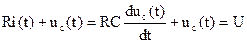Решение этого дифференциального уравнения находится как сумма свободной и принужденной составляющих:

u_c(t) = u_cсв + u_cпр = Вe^pt + U.

Характеристическое уравнение для этой схемы:

pRC + 1 = 0, корень этого уравнения p = –1/RC.

Постоянная времени переходного процесса .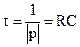

Постоянную интегрирования В найдем, рассмотрев искомую функцию в момент времени t = 0. Так как схема до коммутации была отключена от источника питания, то есть конденсатор не был заряжен, то согласно второму закону коммутации начальное значение напряжения на емкости:

u_c(0+) = u_c(0–) = 0.

Так как u_c(0+)=B + U =0, то В = u_c(0+) – U = –U.

Искомая переходная функция имеет вид:

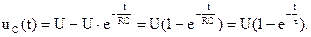
Ток в цепи:

.

Напряжение на резистивном элементе с сопротивлением R:

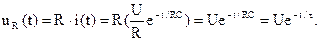
Графики переходных функций тока и напряжений представлены на рис. 6.5.

Рис. 6. 5