Классический метод расчета переходных процессов

Переходные процессы в любой электрической цепи с постоянными параметрами R, L, C описываются дифференциальными уравнениями, составленными в соответствии с законами Кирхгофа для мгновенных значений токов и напряжений.

Решение дифференциального уравнения записывается в виде суммы двух решений: частного и общего. Частное решение неоднородного дифференциального уравнения с постоянными коэффициентами называется принужденной составляющей, а общее решение однородного уравнения – свободной составляющей.

Тогда переходная функция может быть записана:

i(t)=i_св(t)+i_пр, u(t)=u_св(t)+u_пр.

Принужденная составляющая находится путем определения тока или напряжения в установившемся послекоммутационном режиме работы цепи, когда переходный процесс практически закончился (теоретически он длится бесконечно долго). При расчете принужденных значений необходимо помнить, что напряжение на зажимах индуктивной катушки в цепи постоянного тока равно нулю, то есть индуктивная катушка в установившемся режиме в цепи постоянного тока представляет собой проводник с нулевым сопротивлением, а в ветви с конденсатором не протекает постоянный ток и конденсатор, включенный в цепь постоянного тока, представляет собой разомкнутый участок цепи.

Свободная составляющая, то есть решение однородного уравнения, находится как сумма экспоненциальных функций:

i_св(t) =

где А_К – постоянные интегрирования, р_К – корни характеристического уравнения, которые представляют собой постоянные числа, не зависящие от времени. Количество слагаемых определяется числом корней характеристического уравнения.

Характеристическое уравнение можно составить двумя способами.

Первый способ предполагает замену производных искомой функции в однородном дифференциальном уравнении на рⁿ, где n – степень соответствующей производной.

Второй способ состоит в определении входного сопротивления Z(p) относительно любых разомкнутых зажимов пассивной части послекоммутационной схемы, в которой все источники электрической энергии исключены, а реактивные индуктивные и емкостные сопротивления заменяют операторными сопротивлениями Lp и 1/Cp. Полученное выражение приравнивается к нулю, и находятся его корни.

Корни характеристического уравнения всегда отрицательны, поэтому слагаемые свободной составляющей представляют собой затухающие экспоненты.

Постоянные интегрирования А_К находятся с помощью рассмотрения начальных значений искомых функций.

Время переходного процесса зависит от времени затухания свободной составляющей и определяется через постоянную времени τ= 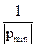. Тогда время переходного процесса t_пп=3÷5τ.