Электрические фильтры
Электрические фильтры – это четырехполюсники, включаемые между источником питания (генератором) и приемником (нагрузкой), назначение которых состоит в том, чтобы без затухания пропускать к приемнику токи одних частот и задерживать или пропускать, но с большим затуханием, токи других частот (рис. 5.4).
   |
Рис. 5.4
Диапазон частот, пропускаемый фильтром без затухания, называется полосой прозрачности (ПП). В идеальном случае необходимо обеспечить нулевое затухание сигнала (коэффициент затухания 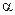 = 0) в этом диапазоне. Диапазон частот, пропускаемый с затуханием называется полосой затухания (ПЗ).
= 0) в этом диапазоне. Диапазон частот, пропускаемый с затуханием называется полосой затухания (ПЗ).
Электрические фильтры выполняют обычно из L и С элементов. В основе их работы лежит зависимость реактивных сопротивлений от частоты:
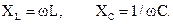
Подключение резисторов с сопротивлением R приводит к подавлению сигналов всех частот, поэтому в пассивных электрических фильтрах они не применяются.
Выполняют фильтры по симметричной Т- или П- образной схеме четырехполюсника, ( 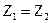 или
или 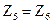 ), согласованного по нагрузке (ZH=ZC). Сопротивления Z1 и Z4 называют продольными, а Z3 и Z5 – поперечными.
), согласованного по нагрузке (ZH=ZC). Сопротивления Z1 и Z4 называют продольными, а Z3 и Z5 – поперечными.
Электрические фильтры, в которых произведение продольного сопротивления на соответствующее поперечное, представляет собой некоторое постоянное для данного фильтра число k, независящее от частоты, принято называть k-фильтрами. Фильтры, у которых это произведение зависит от частоты, называют m-фильтрами.
 |
Фильтры нижних частот (ФНЧ) пропускают сигналы в диапазоне частот от ω1 = 0 до ω2. На рис. 5.4 изображены простейшие П- и Т-образные схемы фильтров низкой частоты.
В этих схемах 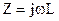 и
и 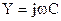 . Индуктивные продольные сопротивления с возрастанием частоты возрастают и гасят высшие гармоники; поперечные емкостные проводимости с увеличением частоты так же возрастают и токи высших гармоник через поперечные ветви возвращаются на вход четырехполюсника.
. Индуктивные продольные сопротивления с возрастанием частоты возрастают и гасят высшие гармоники; поперечные емкостные проводимости с увеличением частоты так же возрастают и токи высших гармоник через поперечные ветви возвращаются на вход четырехполюсника.
Граничные частоты для полосы пропускания определяют из условия:
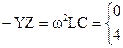 откуда
откуда 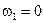 и
и 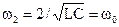 .
.
 На рис. 5.6 показаны зависимости коэффициента затухания a и коэффициента фазы b в зависимости от
На рис. 5.6 показаны зависимости коэффициента затухания a и коэффициента фазы b в зависимости от 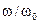 .
.
Фильтры верхних частот (ФВЧ) пропускают сигналы в диапазоне частот от ω1 до ω2= ∞. На рис. 5.7 изображены простейшие П- и Т-образные схемы фильтров, пропускающих сигналы верхних и задерживающие сигналы нижних частот.
 |
В этих схемах 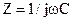 и
и 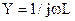 . Продольные емкостные сопротивления при низких частотах имеют большие сопротивления и гасят токи низших гармоник, а при увеличении частоты емкостное сопротивление уменьшается, и высшие гармоники с небольшим затуханием передаются на выход. Продольная индуктивная проводимость имеет большое значение на низких частотах, и токи этих частот через поперечные ветви возвращаются на вход фильтра. На больших частотах проводимость поперечных ветвей уменьшается, и токи высших частот по пути наименьшего сопротивления поступают на выход фильтра.
. Продольные емкостные сопротивления при низких частотах имеют большие сопротивления и гасят токи низших гармоник, а при увеличении частоты емкостное сопротивление уменьшается, и высшие гармоники с небольшим затуханием передаются на выход. Продольная индуктивная проводимость имеет большое значение на низких частотах, и токи этих частот через поперечные ветви возвращаются на вход фильтра. На больших частотах проводимость поперечных ветвей уменьшается, и токи высших частот по пути наименьшего сопротивления поступают на выход фильтра.
 Граничные частоты для полосы пропускания определяют из условия:
Граничные частоты для полосы пропускания определяют из условия:
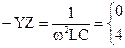 откуда
откуда
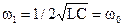 и
и 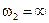 .
.
На рис. 5.8 показаны зависимости коэффициента затухания a и коэффициента фазы b в зависимости от 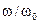 .
.
Полосовые фильтры (ПФ) пропускают сигналы в диапазоне частот от ω1 до ω2 и подавляют сигналы остальных частот. Полосовой фильтр можно получить, если совместить электрически друг с другом схемы фильтров низкой частоты (рис. 5.5) с полосой пропускания ωН1 = 0 до ωН2 и высокой частоты (рис. 5.7) с полосой пропускания ωВ1 до ωВ2 =∞. Тогда полученный фильтр будет пропускать сигналы в диапазоне частот от ωВ1 до ωН2, как показано на частотной характеристике рис. 5.10. На рис. 5.9 приведены две схемы полосовых фильтров, имеющие Т- и П-образные формы.


Чтобы при одной и той же частоте стали равны нулю продольные сопротивления Z (резонанс напряжений) и поперечные проводимости Y (резонанс токов), необходимо выполнить условие, определяющее частоту:
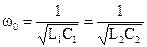 при котором
при котором 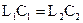 .
.


Заграждающие фильтры (ЗФ) пропускают сигналы в диапазоне частот от 0 до ω1 и от ω2 до ∞, сигналы в диапазоне частот от ω1 до ω2 подавляются. Заграждающий фильтр можно получить если, если совместить электрически друг с другом схемы фильтров низкой частоты с полосой пропускания ωН1 = 0 до ωН2 и высокой частоты с полосой пропускания ωВ1 до ωВ2 = ∞. Тогда полученный фильтр будет подавлять сигналы в диапазоне частот от ωН2 до ωВ1, как показано на частотной характеристике рис. 5.11.


Тогда при частоте ω0 можно получить разрыв продольных сопротивлений Z и короткое замыкание поперечных проводимостей Y. Для этого необходимо выполнить условия:
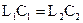 и
и 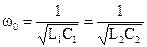 .
.
На рис. 5.12 приведены две схемы заграждающих фильтров, имеющие Т- и П-образные формы.
 |
Дата добавления: 2016-05-25; просмотров: 1795;
