Методы 2-го порядка для решения УУР

Они основываются на сохранении нелинейности при аппроксимации уравнений установившегося режима (2) через квадратичные члены разложения в (14). В этом случае апроксимационная модель имеет вид:

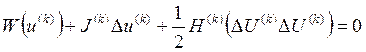(24)

Т.е. исходная нелинейная система уравнений (2) приближенно заменяется квадратичной системой (24).

Более сильная квадратичная аппроксимация по сравнению с линейной в методе Ньютона-Рафсона приводит к более быстрой сходимости и уменьшению времени решения задачи. В методах 2-го порядка на каждой итерации исходная нелинейная система уравнений заменяется квадратичной системой уравнений вида (24) (в отличии от метода Ньютона-Рафсона, в котором исходная нелинейная система заменятся линеаризованной системой вида (23)).

Графически смысл итерационной процедуры 1-го и 2-го порядка рассмотрим на примере одного нелинейного уравнения ω_i=0:

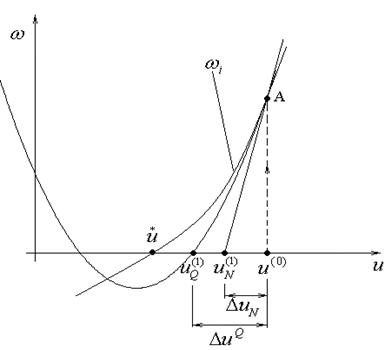
На рисунке:

U^* - искомое точное решение уравнения;

U⁽⁰⁾ – начальное приближение;

U^N- очередное приближение по методу Ньютона-Рафсона;

U^Q - очередное приближение по методам второго порядка.

В методе Ньютона-Рафсона выполняется линейная аппроксимация, т.е. кривая заменяется прямой линией (касательной).

Очередное приближение неизвестных находим: 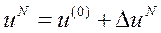. Поправку ΔU^N определяем, решая систему линеаризованных уравнений (23).

В методах 2-го порядка выполняется квадратичная апроксимация, т.е. кривая ω_i заменяется фрагментом параболы.

Очередное приближение неизвестных находим: .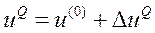

Поправку ∆U^Q находим, решая систему квадратичных уравнений (24).

Методы 2-го порядка дают на каждой итерации более близкое приближение к искомому решению, чем методы 1-го порядка. За счет этого уменьшается общее количество итераций.

Основная сложность методов 2-го порядка состоит в решении системы квадратичных уравнений, получаемых из (24):

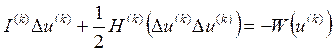. (25)

Эту систему уравнений нужно решать на каждой итерации (вместо линейной системы уравнений (23) в методе Ньютона-Рафсона). Для решения системы квадратичных уравнений применяются итерационные методы, т.е. появляется внутренний итерационный процесс. Эффект от применения методов 2-го порядка определяется способом решения системы квадратичных уравнений. Квадратичная аппроксимация дает значительное сокращение времени расчета. Особенностью метода 2-го порядка является то, что используемая в них квадратичная аппроксимация наиболее адекватно отображает уравнения режима электрической сети. В первую очередь это относится к уравнениям в форме баланса мощности, которые тоже являются квадратичными.