Обобщенный метод Ньютона. Оптимизация в электроэнергетических задачах основывается на следующих группах методов:
Оптимизация в электроэнергетических задачах основывается на следующих группах методов:
· Методы нулевого порядка.
В них не используются производные. Эти методы наиболее медленные, но обладают простыми алгоритмами (метод случайного поиска, метод покоординатного спуска).
· Методы 1-го порядка.
В них используется 1-я производная. Наиболее отработанный и используемый из них - градиентный метод. В нём шаги оптимизации выполняется в направлении антиградиента:
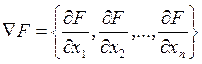
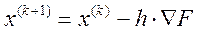 .
.
Составляющими вектора - градиента являются производные от целевой функции по всем управляющим параметрам.
Методы этой группы обладают надежной и быстрой сходимостью.
· Методы 2-го порядка
В них используется 2-я производная. Обладают высокой скоростью сходимости и высокой надежностью.
Суть методов: раскладываем целевую функцию оптимизации F(x) в ряд Тейлора с сохранением производных, включая 2-е производные. При этом выполняется приближенная замена исходной целевой функции F(x) квадратичной (аппроксимирующей) функцией Fоп (разложение Тейлора):
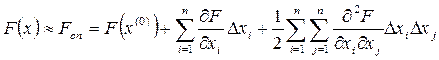 . (1)
. (1)
Минимизация производится по апроксимирующей функции Fоп, т.е. определяем минимум апроксимирующей функции Fоп вместо поиска минимума F(x) . Неизвестными являются поправки ∆Х.
Минимум функциии определяется равенством нулю производных этой функции по всем неизвестным:
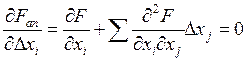 (2)
(2)
В целом для n неизвестных ∆Х получаем систему n уравнений:
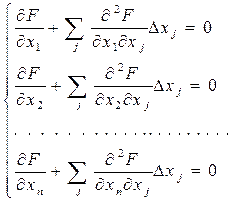 (3)
(3)
Эта система определяем минимум функции Fоп. В матричной форме её мож-но записать:
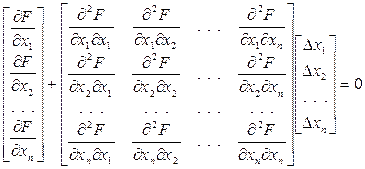 (4)
(4)
или 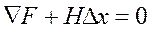 , (5)
, (5)
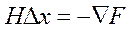 (6)
(6)
Система (6) – линейна относительно ∆Х. Ее решение позволяет определить поправки ∆Х и выполнить очередной шаг оптимизации:
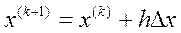 . (7)
. (7)
Определив ∆Х решением системы линейных уравнений (6), можем опреде-лить координаты очередной точки на траектории спуска. Для регулирования длины шага в ходе оптимизации возможно введение коэффициента шага h:
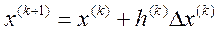 (8)
(8)
Подставляя в (7) значение ∆Х, полученное из (6), получаем общее выражение методов второго порядка для определения координат точки на траектории спуска:
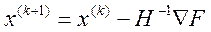 (9)
(9)
Дата добавления: 2016-05-16; просмотров: 626;
