Обобщенный метод Ньютона
Идею метода рассмотрим на примере поиска минимума функции двух переменных F(x1,x2).
Квадратичная аппроксимация в виде (1) приобретает вид:
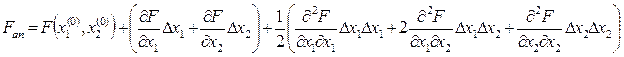
Неизвестные величины здесь - ∆Х1, ∆Х2. Будем определять минимум Fоп.
В точке экстремума градиент функции должен быть равен нулю:
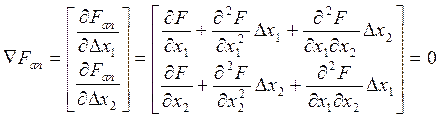 (11)
(11)
Это система линейных уравнений относительно ∆Х1, ∆Х2. Запишем в другом виде:
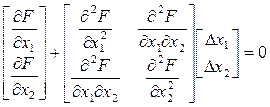 (12)
(12)
Переносим свободные члены в правую часть :
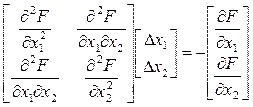 (13)
(13)
Решаем эту систему уравнений, находим ∆Х1, ∆Х2 и далее следующие при-ближения неизвестных.
Геометрическая интерпретация:
В градиентном методе целевая функция апроксимируется касательной к линии равного уровня в точке очередного приближения. Далее шаг выполня-ется в направлении антиградиента.
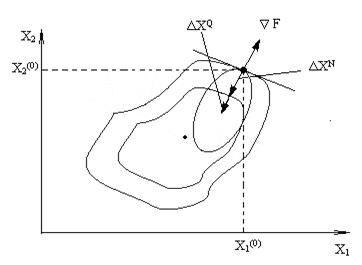
В обобщенном методе Ньютона функция в очередной точке апроксимируется элипсоидом и шаг выполняется к центру этого элипса. Решением системы уравнений (13) отыскивается вектор 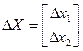 , приводящий к центру элипса. Выполняется квадратичная апроксимация. При этом обеспечивается наилучшая сходимость.
, приводящий к центру элипса. Выполняется квадратичная апроксимация. При этом обеспечивается наилучшая сходимость.
Рассмотрим связь метода оптимизации с методом Ньютона для решения систем нелинейных уравнений.
В точке экстремума функции длина вектора-градиента равна нулю. Составляющие вектора градиента – это производные целевой функции по управляющим параметрам. Значит в точке экстремума функции длина составляющих вектора-градиента также равна нулю:
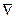 F=
F= 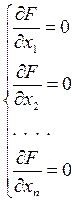 (14)
(14)
Обозначим эти производные в (14) как Ψі :
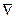 F=
F= 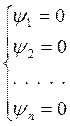 (15)
(15)
Каждая производная представляет собой аналитическое выражение, которое обозначено через Ψ. Получаем нелинейную систему уравнений (15), решив которую мы найдем значения управляющих параметров, соответствующих минимуму целевой функции. Решать ее будем методом Ньютона-Рафсона:
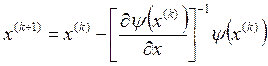 (16)
(16)
Первые производные от Ψ являются вторыми производными от целевой функции F и они образуют матрицу Гессе:
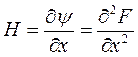
Тогда (16) примет вид:
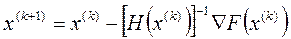 (17)
(17)
Рекурентное выражение обобщенного уравнения Ньютона-Рафсона позво-ляет определить координаты точки на очередном приближении. Матрица Якоби, при решении (15) тождественно равна матрице Гессе. Обобщенный метод Ньютона обеспечивает резкое сокращение шагов оптимизации по сравнению с методами 1-го порядка.
Пример:
Найти минимум функции 2-х переменных
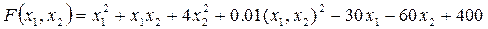
Используем обобщенный метод Ньютона.
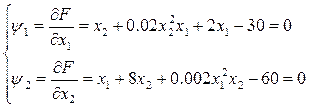 (П2)
(П2)
Обобщенный метод Ньютона соответствует решению системы уравнений (п2) методом Ньютона-Рафсона:
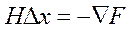 (П5)
(П5)
Определим элементы матрицы Гессе:
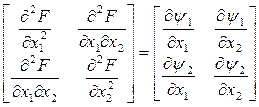 (П3)
(П3)
Дифференцируем Ψ1, Ψ2 по Х1 и Х2:
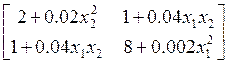
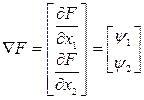 (П4)
(П4)
Зададим начальные приближения неизвестных :

Определим матрицу Гессе в точке начального приближения:
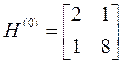
Определим вектор градиент
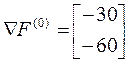
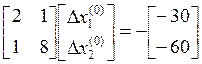 (п5)
(п5)
Решаем эту систему уравнений и находим
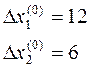
Определим очередные приближения
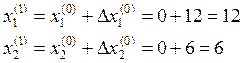
Определим значение целевой функции в новой точке:
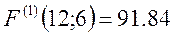
Выполняем второй шаг при нових значениях управляющих параметров
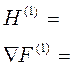
Формируем систему вида(п5), решаем ее и т.д..
Дата добавления: 2016-05-16; просмотров: 2047;
