Решение уравнений установившегося режима методами 2-го порядка

Описание установившегося режима электрической сети наиболее эффективно осуществляется с помощью уравнений установившегося режима. В общем виде это уравнения с комплексными неизвестными, комплексными коэффициентами и свободными членами.

В общем виде систему уравнений установившегося режима можно записать в виде вектор - функции

W(x,y) =0, (1)

где Х - вектор независимых параметров, Y-вектор зависимых параметров. Так как при расчетах установившегося режима независимые параметры постоянны, а зависимые параметры – это, как правило, напряжения в узлах, то можно записать:

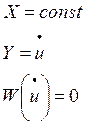(2)

Используются различные формы уравнений установившегося режима:

1. В форме баланса токов

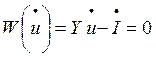. (3)

Здесь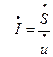

2. В форме баланса мощностей

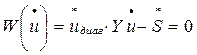(4)

Уравнения установившегося режима в общем случае нелинейны. Решать их можно только итерационными методами.

Итерационные процессы в общем виде можно описать рекуррентной формулой

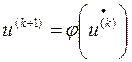. (5)

Здесь φ – описывает определенные действия над U^*(k) , в результате которых получаем очередное приближение неизвестных.

Рассмотрим одно i-е уравнение из системы уравнений (2)

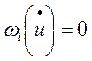(6)

Разложим это уравнение в ряд Тейлора с сохранением производных не выше 2-го порядка:

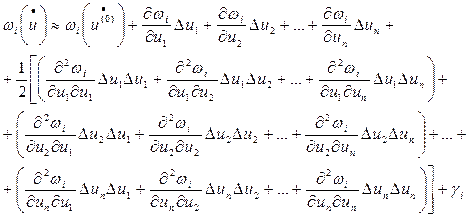(7)

В этом уравнении γ_i – остаточный член разложения, включает в себя все элементы разложения, содержащие производные выше 2-го порядка;

n - количество неизвестных;

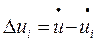– малое приращение неизвестных;

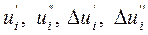- составляющие напряжения и приращения в прямоуголь-

ных координатах;

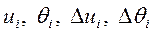- составляющие напряжения и приращения в полярных

координатах;

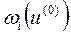– невязка i-го уравнения в точке разложения.

Такое разложение уравнения установившегося режима в ряд Тейлора соответствует приближенной замене его уравнением более простой структуры.

Запишем уравнение (7) в компактном виде:

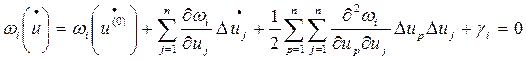(8)

В уравнениях (7) и (8) совокупность первых производных вида 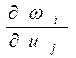соответствует i-й строке матрицы Якоби:

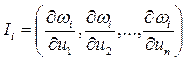. (9)

тогда второе слагаемое в выражении (8) можно записать: 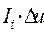, (10)

где ΔU – вектор приращений

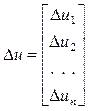. (10а)

Вторые производные в выражении (8) являются элементами матрицы Гессе для i-го уравнения:

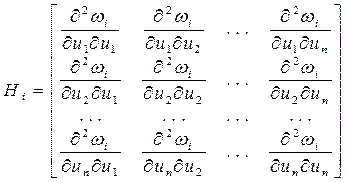(11)

Эта матрица Гессе (11) соответствует одному i-му уравнению системы (2). Каждая её строка - это производные от одного элемента i-й строки матрицы Якоби (9) по всем неизвестным.

С учетом (10а) и (11), слагаемое 3 в выражении (8) можно записать:

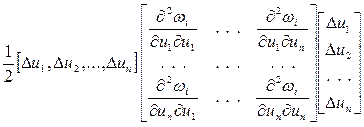, (12)

или в более компактном виде:

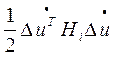(12a)

Тогда выражение (8) с учетом (10) и (12а) можно записать в общем виде: 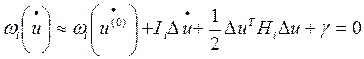, (13)

где ΔU - вектор столбец приращений неизвестных с элементами ΔU_i;

ΔU^Т – вектор-строка приращений;

І_i - строка матрицы Якоби, соответствующая i-му уравнению;

H_i - элемент матрицы Гессе, соответствующий i-му уравнению,

размерность n * n;

γ_i - остаточный член разложения.

При разложении в ряд Тейлора всех уравнений системы (2) получаем систему n матричных уравнений вида (13). При записи этой системы в компактном виде, вместо одной невязки уравнений ώ_i получаем вектор невязок, вместо одной строки матрицы Якоби, получаем полную матрицу Якоби, вместо элемента матрицы Гессе H_i получаем полную матрицу Гессе, γ_i заменяется вектором остаточных разложений.

С учетом этого система уравнений (2) принимает вид:

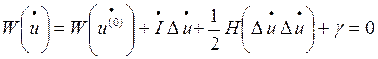(14)

Здесь І - полная матрица Якоби, квадратная размерностью n*n;

Н – полная матрица Гессе, прямоугольная размерностью n*n² , причем

каждая i-я строка матрицы Н формируется из всех строк матрицы

H_i;

(ΔUΔU) – вектор столбец с элементами ΔU_i ΔU_j. Число элементов - n²:

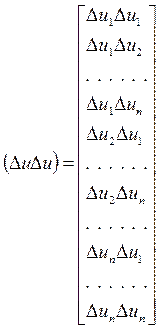
В зависимости от числа членов ряда Тейлора, используемых для аппроксимации системы уравнений установившегося режима (2) в виде (14), получаем методы решения систем уравнений нулевого, первого и второго порядка.

В уравнении (14) пренебрегаем остаточным членом g. Он включает в себя элементы разложения в ряд Тейлора, содержащие производные выше второй. Эта величина относительно мала. В результате, (14) превращается в приближенное равенство, то есть уравнения исходной системы (2) приближенно апроксимируются уравнениями вида (14).