Градиентный метод оптимизации режимов ЭЭС
Суть метода.
Задаем начальное приближение вектора независимых переменных (управляючих параметров) Х. Комплексная оптимизация режима электроэнергетической системы по всем переменным предполагает выбор оптимальных значений следующих управляющих параметров:
· Активных мощностей электростанций в узлах Рi;
· Напряжение в опорных генераторных узлах Ui;
· Реактивная мощность генерирующих источников Qi;
· Коэффициенты трансформации трансформаторов kт.
Все эти параметры при оптимизации рассматриваются, как независимые переменные. За счет изменения их значений добиваются оптимального режима работы ЭЭС.
При оптимизации в качестве управляющих параметров могут приниматься:
1) все параметры из всех перечисленных групп;
2) отдельные параметры из некоторых групп;
3) часть параметров из нескольких групп.
Например: Q10 , Q15;KT5 , P1.
Рассчитываем установившийся режим при заданных параметрах. При этом условие минимума целевой функции (ÑF=0) как правило не выполняется, по- этому нужно в пространстве управляющих параметров выполнять шаги DХ(k) с целью приближения к минимуму целевой функции. В результате выполне-ния очередного шага получаем новую точку на траектории спуска. Далее делаем следующий шаг
х(к+1) = х(к) + Dх(к) , (1)
и т.д. В результате получаем последовательность точек в пространстве управляющих параметров х(0), х(1), …, х(к), …, х(n), образующих траекторию спуска к искомому минимуму целевой функции.
В градиентном методе выполняем движение в направлении антиградиента и поэтому шаг определяется 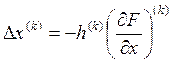 .
.
Знак «-» говорит о направлении антиградиента;
h - коэффициент шага, позволяет изменять длину шага;
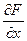 – вектор-градиент.
– вектор-градиент.
Составляющими вектора-градиента при этом являются частные производные от целевой функции по управляющим параметрам.
Подставляем DХ(k) в формулу шага (1):
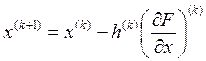 . (2)
. (2)
Это рекуррентное выражение градиентного метода.
Коэффициент шага h при оптимизации может приниматься постоянным либо переменным. При выборе постоянного значения его задают в начале расчета с возможностью корректировки на последующих шагах 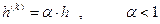 .
.
Начальное значение h целесообразно выбирать таким, чтобы составляющие 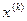 и
и 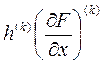 стали приблизительно одного порядка.
стали приблизительно одного порядка.
При задании переменного коэффициента шага, вычисляется его оптимальное значение на каждом шаге оптимизации. Это требует выполнения «пробных шагов» оптимизации и большого числа дополнительных расчетов, но при этом может уменьшатся число основных шагов оптимизации.
Шаги оптимизации выполняются до тех пор, пока длина вектора градиента не станет соизмерима с заданной точностью.
Графическая интерпретация градиентного метода
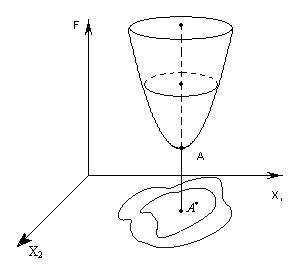
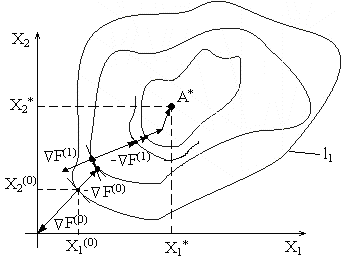
А* - проекция точки минимума целевой функции А на плоскость х1-х2. В результате оптимизации нужно определить ее координаты (Хi*, Х2*).
( 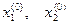 ) – точка начального приближения. Этой точке соответствует линия равного уровня l1. Проводим касательную к линии равного уровня в точке начального приближения. Строим перпендикуляр к касательной. На нем откладываем вектор-градиент ÑF(0). Он направлен в сторону возрастания целевой функции. Шаг оптимизации выполняем в противоположном направлении – направлении антиградиента
) – точка начального приближения. Этой точке соответствует линия равного уровня l1. Проводим касательную к линии равного уровня в точке начального приближения. Строим перпендикуляр к касательной. На нем откладываем вектор-градиент ÑF(0). Он направлен в сторону возрастания целевой функции. Шаг оптимизации выполняем в противоположном направлении – направлении антиградиента 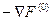 . В результате получаем новую точку с координатами (Х1(1), Х2(1) ). Ей соответствует линия равного уровня l2. Далее действия повторяются. В результате выполнения определенного количества шагов приближаемся к искомой точке минимума целевой функции с заданной точностью.
. В результате получаем новую точку с координатами (Х1(1), Х2(1) ). Ей соответствует линия равного уровня l2. Далее действия повторяются. В результате выполнения определенного количества шагов приближаемся к искомой точке минимума целевой функции с заданной точностью.
Если шаги оптимизации большие, то возможно расхождение процесса оптимизации, т. е. можем « проскочить» точку минимума целевой функции. Если шаги оптимизации очень маленькие, то потребуется очень большое количество шагов для попадания в точку минимума. Поэтому нужно корректировать длину шага в процессе оптимизации, изменяя коэффициент шага h в рекуррентной формуле градиентного метода.
Обобщенный алгоритм градиентного метода оптимизации режима ЭЭС
1. Расчет исходного установившегося режима работы электрической сети при заданных начальных значениях управляющих параметров 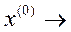 Х(к).
Х(к).
2. Определение составляющих вектора-градиента целевой функции  при этом режиме. В результате вектор-градиент будет полностью определен, то есть будут известны его длина и направление.
при этом режиме. В результате вектор-градиент будет полностью определен, то есть будут известны его длина и направление.
3. Выполнение оптимизационного шага в направлении антиградиента 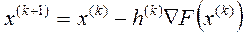 ,
,
где 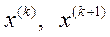 - векторы координат текущей и новой точки на траектории спуска, h – коэффициент шага,
- векторы координат текущей и новой точки на траектории спуска, h – коэффициент шага, 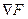 - вектор-градиент. В развёрнутом виде эту формулу можно записать:
- вектор-градиент. В развёрнутом виде эту формулу можно записать:
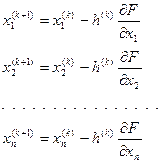
4. Анализ окончания оптимизационного процесса. Возможны 2 варианта: а) сравнение значения целевой функции на смежных шагах. Такой подход является не надежным, если целевая функция является пологой вблизи точки минимума;
б) основан на анализе длины вектора-градиента.
По мере приближения к точке минимума целевой функции, длина вектора градиента и его составляющих уменьшается. В точке минимума длина вектора-градиента равна нулю. 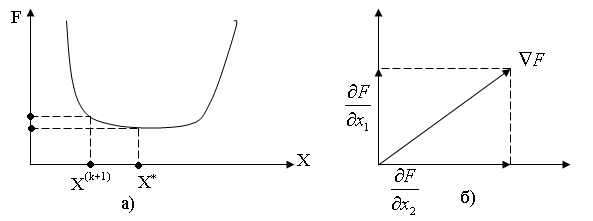
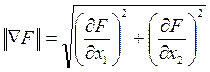
Длина вектора-градиента ( к-норма вектора) определяется через его составляющие и равна корню из суммы их квадратов. В общем случае:
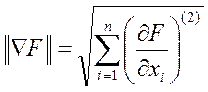
При завершении оптимизации длина вектора градиента (к-норма вектора) должна быть £ e:
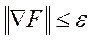 .
.
Если это условие выполняется, то значения управляющих параметров Х(к+1), найденные на текущей итерации, являются их искомыми значениями, при которых достигается минимум целевой функции с заданной точностью. Если условия не выполняются, тогда переход к п.5.
5. Расчет режима при новых значениях управляющих параметров и переход к п.2.
Алгоритм градиентного метода включает 2 крупных расчетных блока:
1) расчет установившегося режима (желательно методом Ньютона-Рафсона); 2) определение составляющих вектора-градиента – производных от целевой функции по управляющим параметрам.
Пример: Оптимизация распределения реактивных мощностей градиентным
методом
Задано:
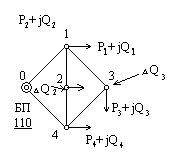
1. конфигурация электрической сети;
2. параметры ее элементов в виде продольных проводимостей участков;
3. напряжение в балансирующем узле U0=Uб=110 кВ;
4. мощности в узлах.
| Узел | P(мВт) | Q(МВАр) |
Необходимо определить оптимальный по потерям активной мощности в сети режим, получаемый за счет регулирования реактивной мощности Q2 и Q3. Реактивная мощность Q2 и Q3 изменяются без ограничений, т. е. введя и изменяя добавки DQ2 и DQ3 можно регулировать режим и добиться оптимального режима.
Таким образом, критерий оптимизации – суммарные потери активной мощности в сети П, управляющие параметры - реактивные мощности Q2 и Q3. Задачу решаем градиентным методом.
Вектор независимых переменных Х: Вектор зависимых переменных Y:
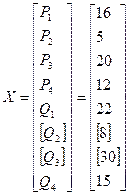
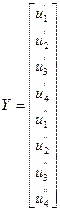
Целевая функция – зависимость суммарных потерь активной мощности. Существует несколько формул определения суммарных потерь мощности. Одна из них:
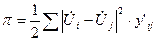 .
.
Для заданной схемы её можно записать:
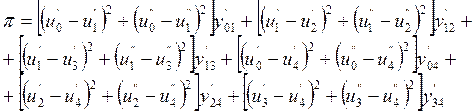 (П1)
(П1)
Вектор градиент включает две составляющие – производные от потерь мощности π по мощностям Q2 и Q3 . Его структура:
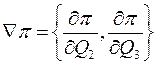 (П2)
(П2)
Для их определения понадобятся уравнения установившегося режима в форме баланса токов. Для заданной схемы система таких уравнений имеет вид:
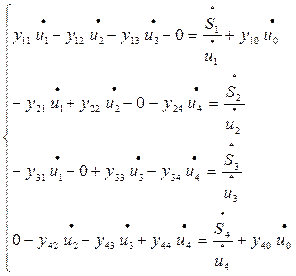 (П3)
(П3)
Это уравнения с комплексными неизвестными и комплексными коэффициентами при неизвестных. Их нужно преобразовать, а именно представить неизвестные напряжения в прямоугольных координатах 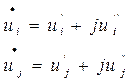 .
.
Затем разделить действительные и мнимые части, при этом каждое комплексное уравнение распадается на 2 действительных. Полученные 8 уравнений будем использовать для определения производных от активных и реактивных мощностей по напряжению.
В алгоритме градиентных методов присутствуют 2 крупных расчетных блока:
1) расчет установившегося режима сети;
2) определение составляющих вектора-градиента.
Для определения производных используем рассмотренную раннее методику ООПП. Составляем пары уравнений в частных производных для узлов с управляющими параметрами узлы 2 и 3: 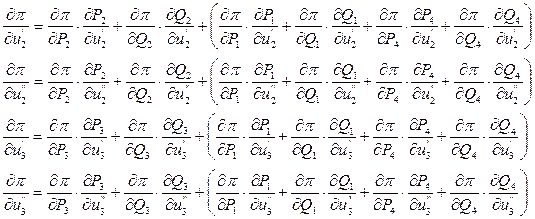 (П4)
(П4)
В общем случае такие пары уравнений нужно записать для всех узлов сети, кроме балансирующего.
Примечания:
1. В скобках записаны слагаемые, относящиеся к узлам 1 и 4, которые непосредственно связаны с рассматриваемыми узлами 2 и 3;
2. Производные от мощностей
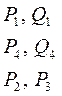
по напряжениям
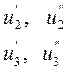
могут быть определены из уравнений установившегося режима, получаемых из (П3). В нашем примере эти производные примем равными нулю, т.к. перечисленные мощности постоянны и не зависят от напряжения.
В результате система (4) приобретает вид :
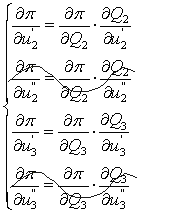
Получаем систему из 4-х уравнений с 2-я неизвестными 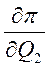 и
и 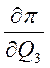 , т.е. переопределённую систему уравнений.
, т.е. переопределённую систему уравнений.
Исключаем любые 2 уравнения (например, 2 и 4). Из оставшихся получаем общие формулы для определения искомых производных:
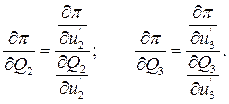 (П5)
(П5)
Производные в числителе (П5) можно получить, продифференцировав целевую функцию (П1) по составляющим напряжения:
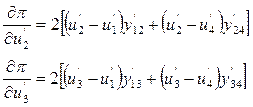 (П6)
(П6)
Производные в знаменателе (П5) можно получить, продифференцировав уравнения установившегося режима, получаемые из (П3):

(П7)
Формулы (П6) и (П7) включают только собственные и взаимные проводимости и напряжения, т.е. производные могут быть вычислены по результатам расчёта режима. После этого можно определить составляющие вектора-градиента по формуле (П5).
Реализуем алгоритм градиентного метода.
Первый шаг ( К=1).
1. Расчет установившегося режима при заданных начальных значениях управляющих параметров. Полученные значения напряжений заносим в таблицу:
| Шаг оптимизации | ||||||
| Параметры режима | ||||||
| Q2 Q3 | 8,74 39,18 | 9,16 38,74 | 1,01 -13,433 | |||
| U1’ U1’’ | 107,93 | 108,84 -0,01 | 108,84 -0,01 | |||
| U2’ U2’’ | 107,93 | 108,86 -0,01 | 108,88 -0,01 | |||
| U3’ U3’’ | 107,39 | 109,0 -0,01 | 108,96 -0,01 | |||
| U4’ U4’’ | 108,21 | 109,06 -0,01 | 109,05 | |||
| p(кВт) | 1,02 | 0,427 | 0,42 | |||
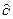 p/ p/ 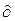 Q2 Q2
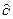 p/ p/ 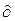 Q3 Q3
| -0,000742 -0,00918 | -0,00042 0,000468 | 0,000118 -0,000127 | |||
| ½½ Ñp½½ | 92,1*10-4 | 6,29*10-4 | 1,1868*10-4 | |||
Определяем суммарные потери активной мощности. Результаты заносим в таблицу.
2. Определяем составляющие вектора-градиента целевой функции по формулам (П6), (П7), (П5):
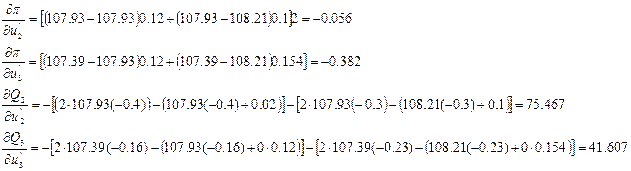
Теперь можем определить составляющие вектора-градиента по (П5)6
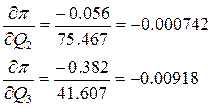
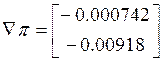
3. Выполняем шаг оптимизации и определяем новые значения управляющих параметров:
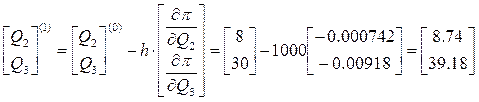
Коэффициент h=1000 выбираем таким, чтобы сделать составляющие в формуле соизмеримыми по величине.
4. Анализируем условия завершение процесса оптимизации:
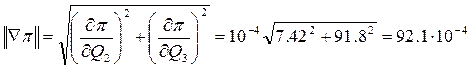 .
.
Все результаты заносим в таблицу.
Второй шаг оптимизации (К=2).
1. Расчет режима и потерь при новых значениях управляющих параметров. Результаты заносим в таблицу. Напряжения в узлах повысились, суммарные потери понизились.
2. Определяем составляющие вектора-градиента в новой точке:


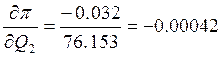
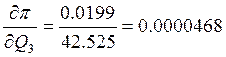
3. Выполняем шаг оптимизации:
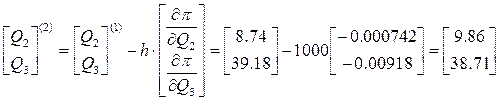
4. Определяем длину вектора-градиента и проверяем условия завершения процесса оптимизации:
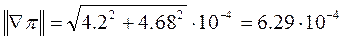 .
.
Следующий шаг выполняем при новых значениях управляющих параметров. Его результаты также заносим в таблицу. В результате выполнения нескольких шагов оптимизации определяем значение управляющих параметров Q2 и Q3, при которых достигается минимум целевой функции – суммарных потерь активной мощности в сети.
Для большей наглядности хода процесса оптимизации рисуют графики изменения основных параметров: управляющих параметров, целевой функции и длины вектора-градиента:

 Q2, p
Q2, p
 Q3
Q3


 1
1



 40 Q3
40 Q3
 30 Q2
30 Q2
 20 0,5
20 0,5







 10
10
 1 2 3 4 К 1 2 3 K
1 2 3 4 К 1 2 3 K


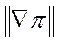 * 10-4
* 10-4
 |  |
 K
K
1 2 3
Учет ограничений в форме равенств в градиентных методах. Метод приведенного градиента (МПГ)
Учет ограничений в виде равенств возможен с помощью неоп-ределенных множителей Лагранжа. При этом ограничения вводятся в состав целевой функции. Это увеличивает размерность задачи и усложняет расчеты за счет появления дополнительных параметров – неопределённых множителей Лагранжа.
В градиентных методах учет ограничений в виде равенств
осуществляется при расчете составляющих вектора-градиента, за счет учета неявной зависимости Y(x) зависимых параметров от независимых. Эта связь между параметрами выражается через уравнения установившегося режима, которые рассматриваются как ограничения в виде равенств:
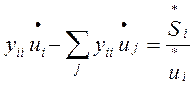 (1)
(1)
Неизвестные напряжения Ui, Uj – зависимые параметры – элементы вектора Y; Si – независимые параметры – элементы вектора Х.
Целевую функцию F(x,y) можно представить:
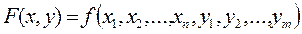 (2)
(2)
Связь между её параметрами может быть описана вектор-функцией ограничений в виде равенств 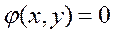 (уравнения связи) или
(уравнения связи) или
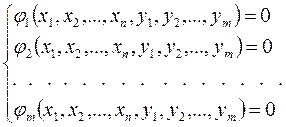 (3)
(3)
Найдем связь между приращениями зависимых параметров DY и независимых параметров DХ.
Рассмотрим точку с координатами (Х(0), Y(0)) в пространстве параметров режима.
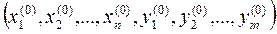 (4)
(4)
Эти значения (Х(0), Y(0)) принимаем удовлетворяющими системе (3), т.е. они являются решением этой системы уравнений.
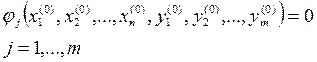 (5)
(5)
Разложим уравнение системы (3) в точке (Х(0), Y(0)) в ряд Тейлора. Ограничимся только линейными членами разложения, т.е. содержащими производные не выше 3-го порядка:
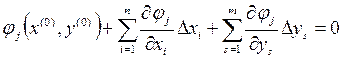 (6)
(6)
Составляющая j(Х(0),Y(0))=0 в соответствии с уравнением (5). Выражение (6) записано для одного j-го уравнения системы. В целом, система уравнений связи (3) при разложении их в ряд Тейлора, в развернутом виде может быть записана:
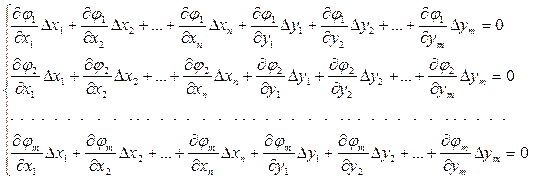 (7)
(7)
В матричном виде система (7) имеет вид:
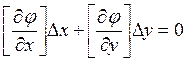 (8)
(8)
Из (8) можно записать:
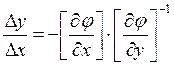 (9)
(9)
Перейдем от малых приращений к производным:
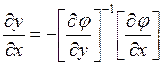 (10)
(10)
В (10) матрица 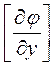 – матрица частных производных от уравнений ограничений в виде равенств по зависимым переменным.
– матрица частных производных от уравнений ограничений в виде равенств по зависимым переменным.
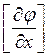 - матрица частных производных от уравнений ограничений в виде равенств по независимым переменным.
- матрица частных производных от уравнений ограничений в виде равенств по независимым переменным.
Выражение (10) определяет связь между зависимыми и независимыми переменными в явном виде. Учитывая неявную связь Y(x), целевую функцию F(x,y), можно представить в виде F(Х,Y(x)) . По правилу дифференцирования сложных функции можно записать:

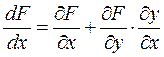 (11)
(11)
Тогда градиент приобретает вид:
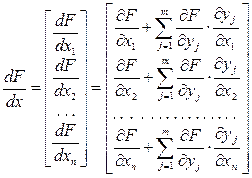 (12)
(12)
Или 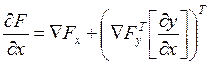 (13)
(13)
Здесь ÑFx и ÑFy – вектор столбцы производных целевой функции по неза-висимым и зависимым параметрам. Подставляем (10) в (13), получаем:
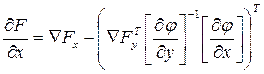 .
.
Вектор производных 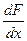 называется приведенным градиентом.
называется приведенным градиентом.
Он рассматривается как возможное направление на каждом шаге оптимизации и используется в градиентном методе в рекуррентном выражении.
Т.о. ограничения в виде равенств учитывается при вычислении вектора-градиента. В остальном алгоритм градиентного метода остался без изменений.
Пример.
Дана целевая функция
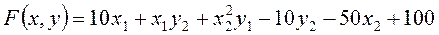 (П1)
(П1)
Заданы ограничения в виде равенств
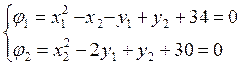 (П2)
(П2)
В качестве независимых параметров принимаем 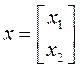 ,
,
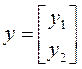 – зависимые параметры.
– зависимые параметры.
Нужно найти минимум функции (П1) с учетом ограничения (П2).
Решение:
1. Метод Лагранжа
Составляем функцию Лагранжа
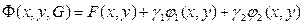 или
или
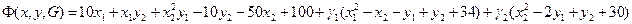 В новой функции 6 неизвестных параметров: Х1,Х2,Y1, Y2, g1,g2.
В новой функции 6 неизвестных параметров: Х1,Х2,Y1, Y2, g1,g2.
Дифференцируем функцию Лагранжа по всем этим параметрам:
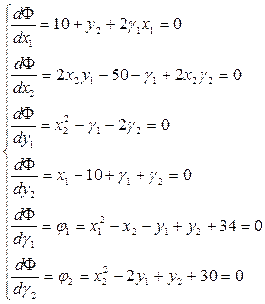
Получаем нелинейную систему 6 уравнений с 6 неизвестными, решаем ее и определяем значения всех параметров. Полученные значения 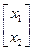 и
и 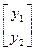 определяют min целевой функции.
определяют min целевой функции.
2. Градиентный метод
Определяем вектор градиент и его составляющие:
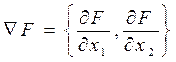
 (П3)
(П3)
1. Зададим начальные приближения управляющих параметров
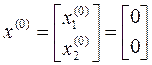
Зависимые переменные y1(0), y2(0) находим из уравнений системы (П2), подставляя туда х1(0), х 2(0) и решив её:
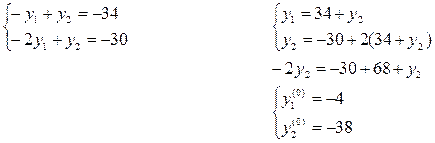
Определяем значение целевой функции в начальной точке, подставляя в (П1) значения х1(0), х 2(0) , y1(0), y2(0) :
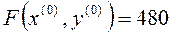
2. Определяем составляющие вектора-градиента, подставляя в (П3) значения параметров:
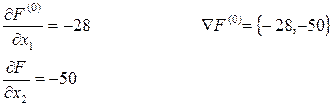
3. Выполняем шаг оптимизации и определяем новые значения управляющих параметров:
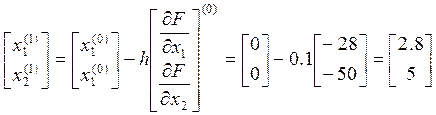
Определяем соответствующие значения зависимых параметров:
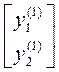
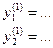
Определяем значение целевой функции в новой точке из (П1) 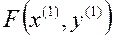 = …
= …
4. Контроль завершения процесса оптимизации
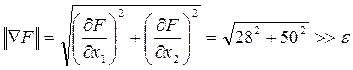
Так как условие не выполняется, то переходим к следующему шагу оптимизации.
3. Метод приведенного градиента
Составляющие вектора градиента определяются по формуле
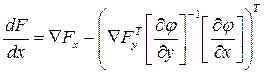
Для рассматриваемого примера формула может быть записана в виде
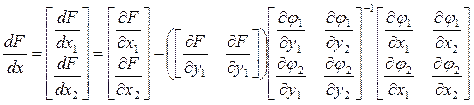
Определим аналитические выражения для всех производных в составе этой формулы:
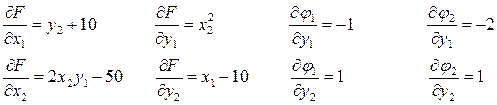
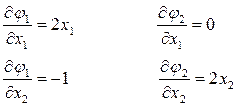
Подставляем найденные значения в формулу:
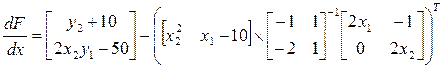 (П4)
(П4)
Реализуем алгоритм градиентного метода: зададим начальные приближения управляющих параметров:
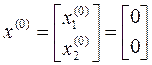
Находим значения зависимых параметров У(0) из системы уравнений связи (П2): 
Значение целевой функции в этой точке 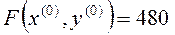 .
.
Определяем составляющие приведенного вектора-градиента по формуле(П4): 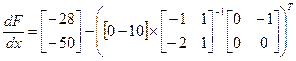 = …
= …
Найденные значения составляющих вектора градиента используем в рекуррентной формуле при выполнении очередного шага оптимизации. Дальнейший алгоритм совпадает с предыдущим методом.
Дата добавления: 2016-05-16; просмотров: 2453;
