Методы определения относительных приростов потерь

В задачах оптимизации режимов электроэнергетических систем исполь-зуются частные производные от суммарных потерь активной мощности в сети по узловым мощностям. Эти производные называются относительными приростами потерь 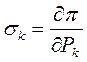(1)

Они рассматриваются как интегральные характеристики режима работы ЭЭС.

Они используются также в градиентных методах оптимизации в качестве составляющих вектора-градиента. Для их расчета можно использовать два принципиально разных подхода:

1. Подход основан на численном дифференцировании потерь:

При этом производные заменяются отношением конечных приростов соответствующих параметров: 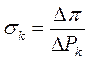(2)

Последовательность расчета:

Определяем исходный режим сети и соответствующие потери π_0. Затем изменяем активную мощность 1-й станции на малую величину DР₁. Снова рассчитываем режим и определяем потери π в этом режиме. Относительный прирост потерь для 1-й электростанции составит:

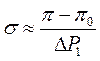(3)

Для получения более точного результата нужно выполнить несколько шагов изменения мощности электростанции на величину DР, определить соответствующее число значений s и найти среднее их значение s₁. Это и есть приближённое значение относительного прироста потерь для 1-й станции.

Такую же последовательность расчета нужно повторить для всех электростанций системы.

Такой расчет очень трудоемкий, так как он требует многократных расчетов режима электросети с высокой точностью. Но он прост алгоритмически.

2. Аналитическое определение s:

Этот подход точный и более универсальный. Методика основана на использовании правил дифференцирования сложных неявных функций.

Для определения производной (1) должна существовать явная зависимость потерь от узловых мощностей. Её удаётся получить только для простых схем. Для общего случая такое выражение получить не удаётся или оно очень сложное. Поэтому задача определения производных (1) разделяется на подзадачи.

Определим аналитическое выражение зависимости суммарных потерь активной мощности от напряжения в узлах. Потери явно зависят от напряжения и могут быть определены по результатам расчета режима:

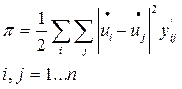(4)

* *

Ui Uj

i j

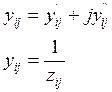
, где y_ij^’ – действительная составляющая продольной

проводимости участка i-j;

Коэффициент ½ - потому - что каждый участок (и потери в нём) входит в сумму 2 раза.

Формула (4) в прямоугольных координатах:

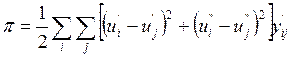(4a)

.

В полярных координатах:

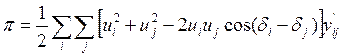, (4б)

где U_i, U_j - модули напряжений в узлах;

d_i, d_j - углы напряжений.

Таким образом, потери активной мощности являются явной функцией напряжения в узлах 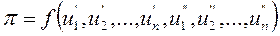. (5)

В то же время напряжения в узлах являются неявной функцией мощностей узлов 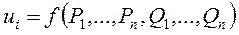. (6)

Эта зависимость представляется в виде систем нелинейных уравнений установившегося режима в форме баланса токов или баланса мощностей:

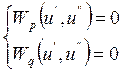(7)

Например, уравнения баланса мощности в прямоугольных координатах ….

Эти уравнения определяют связь между мощностями и напряжениями в узлах. Таким образом, учитывая (5) и (6) можно утверждать, что суммарные потери активной мощности неявно зависят от активной мощности в узлах.

По правилу дифференцирования сложных неявных функций с учетом явных и неявных зависимостей, можно записать для i-го узла:

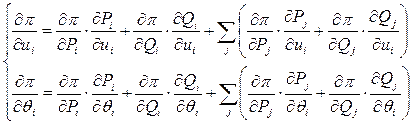(8)

Такие пары уравнений нужно записать для всех узлов сети, кроме балансирующих. Получаем систему из 2n линейных уравнений. В этих уравнениях производные 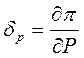и 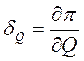– искомые относительные приросты потерь по узловым мощностям. Относительно них - рассматриваемая система уравнений, все остальные производные являются либо коэффициентами при неизвестных либо свободными членами системы уравнений.

Определим выражения для этих производных. Производные в левой части уравнений системы (8) можно получить, продифференцировав по Ui , Qi выражения (4б).

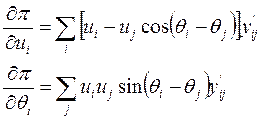(9)

Значения этих производных могут быть вычислены после расчета режима сети и напряжений в узлах. Все остальные производные в правой части системы (8), вида 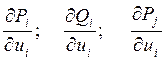и т.д. можно получить, продифференцировав уравнения установившегося режима в форме баланса мощностей по модулям и углам напряжений.

Пример:

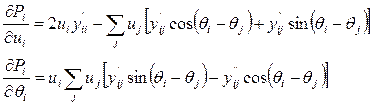(10)

Производные такого вида определяются в при расчёте режима методом Ньютона-Рафсона при формировании матрицы Якоби. В составе этих формул (10) присутствуют только проводимости (y_ii, y_ij,..) и напряжения (U , Q) , то есть значения производных могут быть определены по результатам расчета режима.

После вычисления значений производных по формулам (9) и (10), получаем систему линейных уравнений вида (8), в которой неизвестными являются относительные приросты потерь s_Р и s_Q и известны коэффициенты при них и свободные члены.

В матричном виде эта система имеет вид: 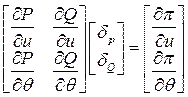(11)

Матрица коэффициентов в системе (11) – это транспонированная матрица Якоби. Решив эту систему линейных уравнений, определяем искомые относительные приросты потерь.

Итог: этот метод определения относительного прироста потерь требует лишь одного расчета установившегося режима. Если расчет режима выполняется методом Ньютона-Рафсона, то элементы матрицы коэффициентов в (11) уже известны (при вычислении матрицы Якоби) и вычисление относительных приростов потерь является простым дополнением к программе расчета установившегося режима.

Этот метод совмещается с любой формой записи уравнений установившегося режима. Например, если эти уравнения заданы в прямоугольных координатах, то система (11) приобретает вид:

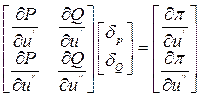(12)

Производные в правой части системы (12) могут быть получены дифференцированием формулы (4а):

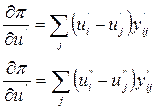(13)

Элементы матрицы коэффициентов в (12) можно определить дифференцированием уравнений установившегося режима в прямоугольных координатах.

Общий алгоритм определения

относительных приростов потерь

1. Расчет установившегося режима электрической сети методом Ньютона-Рафсона;

2. Определение значений производных в точке режима по формулам вида (9), (10);

3. Расчет относительных приростов потерь решением системы уравнений (11) или (12).

Аналогично можно рассчитать относительные приросты потерь по любым другим параметрам, например по коэффициентам трансформации.

Такие производные могут использоваться, также, при оптимизации установившегося режима градиентными методами.