Учет ограничений в виде неравенств

Наибольшие трудности при оптимизации вызывает учет ограничений в виде неравенств на зависимые переменные, то есть ограничения вида: y_i^min≤ y_i ≤y_i^max. Это определяется тем, что связи между управляющими (независимыми) параметрами и зависимыми параметрами являются нелинейными.

Для учета таких ограничений может быть использован приближённый метод Штрафных функций. Суть метода: допускается работа при любых значениях переменных, на которые налагаются ограничения, в том числе и с нарушениями этих ограничений, но в случае нарушения допустимых пределов по какой либо зависимой переменной y_r в целевую функцию вводится большая положительная величина - функция штрафа Ш_r, делающая работу с нарушениями допустимых пределов невыгодной.

Аналог – прогрессивный налог на доходы.

Штрафные функции

Штрафные функции подчиняются следующим условиям:

1. Ш(Y)=0, если Y є D_y

2. Ш(Y)>>0, если Y 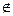D_y , где D_у – допустимая область.

Если соответствующая зависимая переменная удовлетворяет заданным ограничениям, тот штраф =0. В противном случае налагается штраф в виде положительной добавки к исходной целевой функции F(X,Y). Чем больше отклонение от заданных пределов, тем больше величина штрафа.

В электроэнергетических задачах наиболее часто используют квадратичные штрафные функции, которые в общем случае можно записать:

Ш= 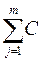j (δу_j)².

Графически квадратичная штрафная функция имеет вид:

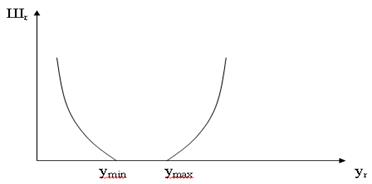
δу_j – характеризует величину отклонения параметра j от заданных

пределов.

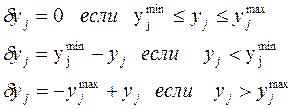
С_j – коэффициент штрафа. Используется для согласования размерности штрафной функции и целевой функции. Зависимые параметры Y могут иметь различную физическую суть (напряжения, токи и т.д.). Для обеспечения их корректного сложения используется коэффициент С.

Например, если рассматриваются ограничения на напряжению и величина отклонения определяется в кВ, то коэффициент С (коэффициент штрафа) в том случае будет иметь размерность 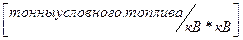и он показывает сколько тонн условного топлива (т.у.т.) добавляется к целевой функции за квадрат отклонения напряжения от допустимого.

В результате введения штрафных функций, целевая функция примет вид: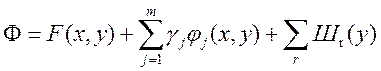

Графически учет ограничений в виде неравенств выглядит следующим образом:

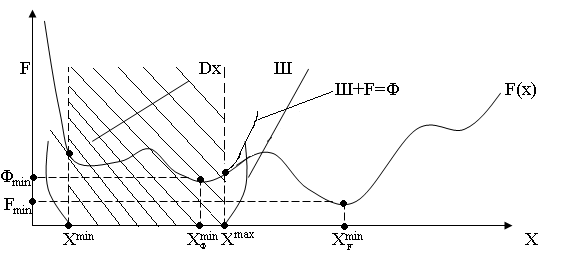
Исходная целевая функция F(x) имеет абсолютный минимум равный F_min при X_min^F. На значения параметра Х налагаются ограничения Х_min£Х£ Х_max. Для их учета используем метод штрафных функций.

Будем искать минимум целевой функции внутри допустимой области D_y. Выполняем графически сложение исходной целевой функции F и штрафной функции Ш. Получаем новую функцию Лагранжа F с абсолютным минимумом внутри допустимой области D_у. Определяя минимум функции F, найдем F_min при Х _min^F, находящимся в допустимой области D_у. При этом в Х _min^F¹ X_min^F ; F_min > F_min. Минимум новой функции Ф переместился в допустимую область параметров и при его определении в процессе оптимизации ограничения учитываются автоматически.

Задача оптимизации сводится к безусловной минимизации функции F по независимым Х и зависимым У параметрам. Условия экстремума функции определяются равенством нулю ее частных производных по всем переменным. Запишем эти условия для функции (5) (условия Куна-Таккера):

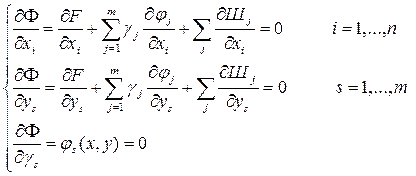(6)

Эти уравнения образуют систему из (n+2m) уравнений (в общем случае нелинейных). Решая полученную систему уравнений , определяем значение всех параметров, в том числе управляющих Х, при которых достигается минимум целевой функцию с учетом ограничений в виде равенств и неравенств (на рисунке _Хф^min).