Учёт ограничений в виде равенств. Метод Лагранжа.

Минимизация функции F(x,y) при ограничениях в виде равенств j(x,y)=0 является классической задачей поиска условного экстремума функции многих переменных.

Один из общих методов решения таких задач заключается в следующем: вместо целевой функции F(x,y), с учетом уравнений связи j(x,y)=0 рассматривается новая функция – функция Лагранжа. Она формируется на основе исходной целевой функции и уравнений связи:

F(X,Y,G)=F(X,Y)+ 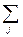γ_j · j_j(X,Y), (1)

где F – исходная целевая функция;

j_j – уравнение ограничений в виде равенств (уравнения связи);

γ_j – дополнительные множители – неопределенные множители

Лагранжа;

F – функция Лагранжа.

Минимум функции Лагранжа совпадает с искомым минимумом функции F(X,Y) с учётом ограничений j(X,Y) т.к. они включены в состав функции Лагранжа и учитываются при этом автоматически.

В этом случае задача нахождения условного экстремума функции F(x,y) заменяется задачей безусловной оптимизации функции Лагранжа, то есть задача поиска оптимального решения при наличии ограничений сводится к задаче определения минимума функции Лагранжа без ограничений.

Экстремум функции может быть найден следующим образом:

1. Дифференцируем функцию по всем переменным;

2. Приравниваем полученные производные нулю;

3. Решаем полученную систему уравнений и определяем значения параметров, при которых достигается экстремум функции.

Запишем эти условия:

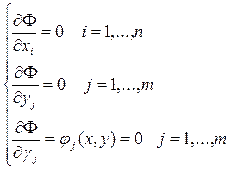(2)

Это условия Куна-Таккера - условия минимума целевой функции.

Запишем условие (2) в развернутом виде:

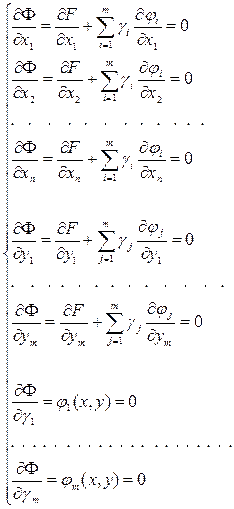
В результате мы получаем систему линейных или нелинейных уравнений, относительно параметров X,Y, γ. Решаем систему любым из известных методов и определяем в результате значения всех параметров, в т.ч. и управляющих параметров Х, которые обеспечивают достижения минимума целевой функции и удовлетворяют ограничениям в виде равенств.

Метод Лагранжа относится к прямым методам. Недостатком этого метода является увеличение размерности задачи за счет введения дополнительных неизвестных γ – неопределённых множителей Лагранжа. Их число равно числу уравнений связи (уравнений ограничений в виде равенств).

Пример:

Задана функция двух переменных – целевая функция:

F=10x₁² – 2x₁ +4x₂ – x₁x₂ +2

Нужно найти его минимум с учетом уравнения связи:

j = x₁ + 10x₂ – 3=0

Параметры 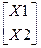- управляющие параметры.

Составляем функцию Лагранжа для заданных условий:

F = F(X) + γj

Подставляем в неё целевую функцию и уравнение связи:

F = 10x₁² – 2x₁ + 4x₂ – x₁x₂ +2 + γ(x₁+10x₂ - 3)

В полученной функции Лагранжа – три параметра: х₁, х₂ и γ.

Будем искать минимум функции Лагранжа. Для этого дифференцируем её по х₁, х₂, γ:

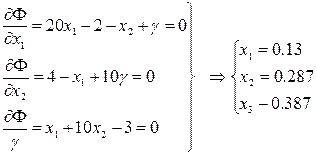
В результате решения полученной линейной системы уравнений определили значения управляющих параметров х₁, х₂ , при которых исходная функция F(х₁, х₂ ) достигает своего минимума с учётом ограничений в виде равенств: F_min = 3,02 .