Основные определения. Экстремумом функции многих переменных F(Х) называется ее минимальное или максимальное значение
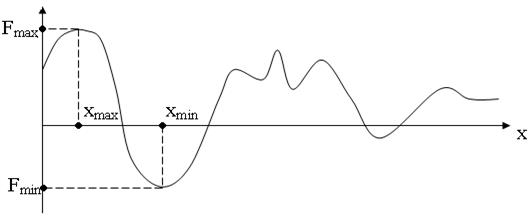
Экстремумом функции многих переменных F(Х) называется ее минимальное или максимальное значение. В общем случае функция может иметь несколько минимумов и максимумов (несколько экстремумов). Один из них - наибольший максимум или наименьший минимум называется глобальным экстремумом, остальные – локальными.
Функция n переменных описывается поверхностью в (n+1)-мерном пространстве.
 |
F F(X1, X2)
Fmin 
l2
l1
А
X*1 X1
X*2 А* l2*
X2 l1* Рис. 2.
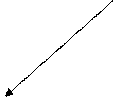
Функция двух переменных F(X1,X2) представлена в трехмерном пространстве. На Рис.2. точке А с координатами (Х1, Х2) соответствует минимум функции Fmin. Пересекая поверхность функции плоскостями, параллельными плоскости X1 - X2 , получаем на ее поверхности ряд линий, которые называются линиями равного уровня. В каждой точке таких линий, функция имеет одно и то же значение. На Рис. 2. – линии l1, l2 .
Линия равного уровня – геометрическое место точек в пространстве независимых переменных Xi (i=1,2,..,n), в которых функция имеет одно и тоже значение Fj=const.
Количество линий равного уровня может быть бесконечным.
На плоскости Х1 – Х2 рассматриваем проекции точки минимума функции А*, проекции линий равного уровня l1* , l2*, …
С поиском экстремума функции связана задача оптимизации. Она заключается в определении экстремального значения функции F(Х) , с учетом ограничений, налагаемых на элементы n-мерного вектора параметров Х:
X={X1, X2, .., Xn} .
Функцию F(Х) называют целевой функцией.
При решении задачи оптимизации в первую очередь определяются значения параметров, при которых обеспечивается экстремум функции. На рисунке это соответствует координатам т. А* (проекция min функции А на плоскость X1- X2).
Ограничения при оптимизации могут быть представлены в виде равенств и неравенств.
Ограничения в виде равенств : j(х)=0 - представляют собой уравнения или системы уравнений ( линейные или нелинейные), которые связывают между собой параметры, являющиеся элементами вектора Х. В этом случае изменение любого из параметров, входящих в уравнение, приводит к соответствующему изменению остальных параметров (чтобы соблюдалось равенство). Например, в уравнении Х1 + Х2 - 10 = 0 при любом значении Х1 (Н-р, 1, 5, 10, …) для соблюдения равенства, значения Х2 могут принимать только соответствующие определённые значения ( 9, 5, 0, …). Т.е. параметры Х1 и Х2 в уравнении связаны между собой, возможности изменения их значений ограничены уравнением. Такие уравнения называют иногда уравнениями связи.
Ограничения в виде неравенств: Ximin £ Xi £ Ximax . Они определяют допустимый интервал изменения параметров. Например, допустимые пределы изменения напряжения в электрической сети U определяются в 5% от номинального Uн :
(Uн – 5% Uн)£ U £(Uн + 5% Uн)
Ограничения в виде неравенств образуют допустимую область Dx
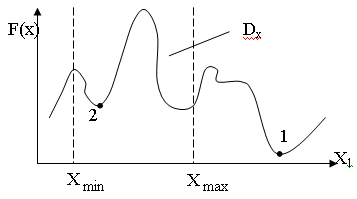
Ограничения в виде равенств или неравенств при оптимизации могут отсутствовать.
Пример:
Целевая функция F(x1,x2)=x1+2x2-x1x2+100
Ограничения в виде равенств j(x1,x2)=x1+x2-10=0
Ограничения в виде неравенств 0 £ X1£ 10
Нужно определить значения параметров х1 и х2, при которых достигается минимум целевой функции F(x1,x2) с учетом ограничений на значения параметров в виде равенств и в виде неравенств.
Абсолютным (безусловным) экстремумом называется точка экстремума функции без учета ограничений в форме неравенств (точка 1).
Условный (относительный) экстремум – точка внутри или на границе допустимой области, в которой функция принимает максимальное или минимальное значение из всех значений внутри этой области (точка 2).
Точка условного экстремума и соответствующее ей значение функции является оптимальным решением задачи.
Общими методами решения задач оптимизации являются методы математического программирования. Математическое программирование при линейной целевой функции F(Х) и линейных ограничениях в виде равенств называется линейным программированием. Математическое программирование при нелинейной целевой функции F(x) или нелинейных ограничениях в виде равенств называется нелинейным программированием.
Общими являются численные методы оптимизации (метод перебора, метод покоординатной оптимизации, градиентные методы и т.д.). Они применимы при любом характере целевой функции и ограничений. Это многошаговые методы.
В этих методах задается исходная точка Х0 с координатами (Х1(0), Х2(0),…,Хn(0)). Для достижения искомой точки минимума выполняется ряд последовательных шагов D Х(к) в пространстве параметров. На каждом шаге решается задача выбора направления шага и его длины. Способом выбора длины и направления различаются методы оптимизации. После выполнения очередного шага получаем координаты следующей точки Х(к+1):
Х(к+1) = Х(к)+D Х(к) .
Совокупность таких шагов образует траекторию спуска к точке минимума целевой функции.
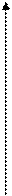x2
Х*
Х(0)
X2(0)
 |
X1 (0) X1
Методы перебора
Это простейшие из методов. Вся допустимая область D представляется в виде многомерной (равномерной) сетки. Узлы этой сетки соответствуют дискретным значениям Х. Вычисляются значения функции в каждом из узлов, и выбирается экстремальное из них F(x1(к), x2(k))
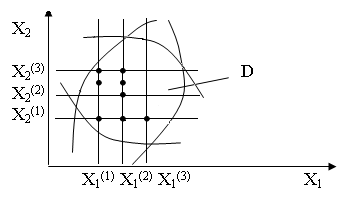
Точность возрастает с уменьшением шага дискретизации, при этом возрастает объем вычислений.
Метод не эффективен при большом количестве n и обширных областях D.
Более эффективны методы направленного перебора и среди них метод покоординатной оптимизации.
В любом из методов, при выполнении шага оптимизации X1(1) = X1(0)+D X1
каждая новая точка должна быть лучше предыдущей:
F(x1(1), x2(1))< F(x1(0), x2(0)),
F(x1(2), x2(2))< F(x1(1), x2(1)), … .
Т.е. значения целевой функции должны уменьшаться (если определяется минимум функции).
X2 В методах покоординатной
оптимизации шаги оптимизации
выполняются вдоль осей координат.
X*
 | |||
 |
X2(0)
X2(1)
X1
X1(0) X1(1) X1(2) X1(3)
Дата добавления: 2016-05-16; просмотров: 688;