Электрических станций методом Лагранжа
Задача оптимального распределения активных мощностей электростанций рассматриваются как одна из самостоятельных задач оптимизации.
Постановка задачи:
Рассматриваем электроэнергетическую систему, состоящую из nс тепловых станций, электрической сети и нагрузок потребителей в виде постоянных мощностей. Все переменные мощности электростанций должны удовлетворять условию баланса активных мощностей
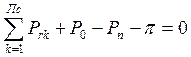 (1)
(1)
Здесь Ргк – активная мощность генерации на к-й станции;
Р0 - активная мощность балансирующего узла;
РН – суммарная активная мощность нагрузки;
π – суммарные потери активной мощности в сети.
Это уравнение рассматриваем как ограничение в виде равенств при оптимизации. В качестве критерия оптимальности работы энергосистемы будем рассматривать суммарный расход условного топлива на электростанциях, необходимый на выработку заданного количества электроэнергии
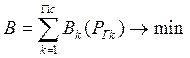 (2)
(2)
Вк (Ргк) – расход топлива на каждой электростанции.
Его можно записать в денежном выражении 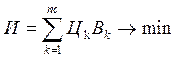
И – издержки на топливо;
Цк – цена на топливо для данной электростанции.
Каждая электростанция имеет свою характеристику экономичности:
 | |||
 | |||
 В
В
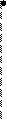 |

 1
1

 2
2

 3
3
 |
Р3 Р2 Р1 Р
Суммарный расход топлива на электростанциях зависит от распределения нагрузок между станциями. Задача состоит в том чтобы определить такие нагрузки Ргк каждой электростанции, при которых суммарный расход топлива (или суммарные затраты) является минимальным с учетом условия баланса активных мощностей в системе (1).
Таким образом, целевая функция оптимизации – суммарный расход топлива на электростанциях ΣВк(Ргк), ограничения в виде равенств - условие баланса активных мощностей в системе (1).
Для решения задачи используем метод Лагранжа. Метод прямой. С учетом (2) и (1) сформируем функцию Лагранжа
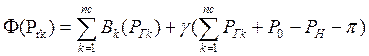 (3)
(3)
Запишем условие минимума целевой функции (условие Куна-Таккера)
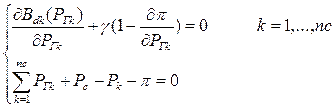 (4)
(4)
Система уравнений (4) описывает оптимальное распределение активных мощностей в энергосистеме.
В её составе есть важные производные:
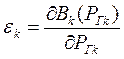 (5)
(5)
Это характеристика относительного прироста (далее ХОП) расхода топлива на к-й электростанции на единицу дополнительной активной нагрузки этой станции. Другими словами ХОП показывает, на сколько изменяется расход топлива на электростанции при изменении ее нагрузки (например на 1 МВт). Эта величина eк(Ргк) может быть представлена графически или аналитически. Она индивидуальна для каждой электростанции.
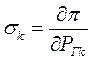 (6)
(6)
Это относительный прирост потерь для к-й станции.
Эта величина характеризует изменение суммарных потерь активной мощности в сети π при изменении активной нагрузки к-й станции на 1 МВт. Эта величина рассматривается как самостоятельная интегральная характеристика эффективности режима работы электрической сети. Ее определение – сложная задача.
С учетом принятых обозначений (5) и (6) и при учете зависимости потерь активной мощности в сети от распределения нагрузок между электростанциями, условие (4) можно записать:
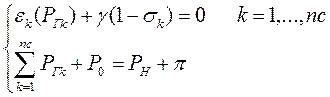 (7)
(7)
или
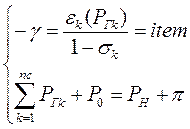 (8)
(8)
При любых k отношение (8) будет постоянно и равно g. Решая систему уравнений (8), определяем значение активных мощностей станций Ргк , при которых обеспечивается минимальный расход топлива на электростанциях на производство и передачу электроэнергии с учётом баланса активных мощностей в сети.
Упрощенный алгоритм распределения суммарной активной мощности между электростанциями
1. Выбор начальных приближений мощностей Ргк(0) (управляющие параметры), а также g(0) – неопределенный множитель Лагранжа;
2. Расчет установившегося режима электрической сети. Определение суммарных потерь активной мощности π, определение относительных приростов потерь sk и мощности балансирующего узла Р0;
3. Определение относительных приростов расхода топлива eк для каждой электростанции, которые соответствуют вычисленным приближениям мощностей электростанций;
4. Определение очередных приближений мощностей электростанций Ррк(i) из 1-го уравнения системы (7);
- Определение небаланса активной мощности w :
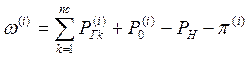
- Проверка условия завершения оптимизации
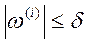 . Если условие выполняется, то оптимизация завершена. Если условие не выполняется, то – определение очередного приближения g(i+1) по формуле Ньютона
. Если условие выполняется, то оптимизация завершена. Если условие не выполняется, то – определение очередного приближения g(i+1) по формуле Ньютона 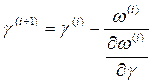 и переход к п.2
и переход к п.2
Аналогично может рассматриваться задача распределения реактивных мощностей источников. Но, так как генерация реактивной мощности Q не связана с затратами на топливо, то цель распределения реактивных мощностей – снижение суммарных потерь активной мощности в сети.
Дата добавления: 2016-05-16; просмотров: 732;
