Силы, действующие на частицы сплошной среды

Сплошная среда движется и деформируется под действием сил, приложенных к составляющим ее частицам.

Для характеристики этих сил выделим некоторый объем сплошной среды 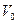(рис. 1.5), ограниченный замкнутой поверхностью 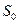. Внешние силы, действующие на частицы среды, делятся на два вида: массовые и поверхностные.

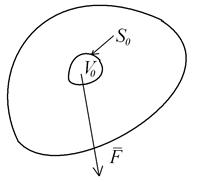
Рис.1.5. К введению массовых и поверхностных сил,

действующих на сплошную среду

Массовые силы действуют на каждую частицу, находящуюся внутри объема 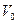, независимо от того, как далеко она расположена от поверхности 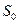. Примером таких сил может служить сила тяжести, электромагнитные силы, силы инерции.

Поверхностные силы представляют собой силы сцепления между частицами, вошедшими в объем 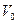, и остальной частью среды. Эти силы распределены по поверхности 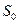выделенного объема, в силу чего они названы поверхностными. На внешней поверхности тела (в этом случае 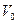представляет объем всего тела) поверхностные силы отражают взаимодействие тела с окружающей средой.

Дадим более подробную характеристику этих двух видов сил.

Массовые силы. Рассмотрим в окрестности точки 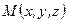элементарный объем 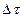сплошной среды, масса которой равна 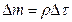. Пусть со стороны внешних тел на частицы, входящие в объем 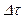, действует суммарная сила 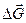. Тогда сила, рассчитанная на единицу массы равна 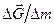. Стягивая элементарный объем к точке 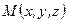, найдем предел

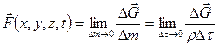. (1.17)

Величина 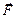этого предела называется вектором плотности массовых сил. Иными словами, плотность массовых сил – это массовая сила, рассчитанная на единицу массы среды.

Плотность массовых сил 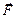есть векторная величина, имеющая размерность ускорения:

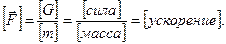
Суммарная массовая сила 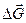, действующая на среду, заключенную в объеме 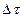, равна 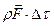, а сила, действующая на конечный объем 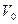, представляется интегралом

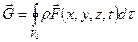. (1.18)

Поверхностные силы. Несмотря на то, что реальные материалы состоят из отдельных частиц, благодаря силам внутреннего взаимодействия (силам сцепления), они не рассыпаются на отдельные части, а существуют в том или ином агрегатном состоянии. С целью учесть это важное обстоятельство и дать количественную характеристику силам сцепления поступим следующим образом.

Рассмотрим произвольную точку 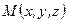сплошной среды, и мысленно проведем через нее элементарную площадку 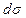(рис. 1.6), характеризуемую единичным вектором нормали 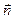. Эта площадка разделяет частицы сплошной среды, находящиеся в окрестности точки 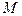, на две группы: те, что находятся с той стороны площадки, куда указывает единичный вектор 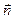(1-ая группа), и те, что находятся с другой стороны площадки (2-ая группа).

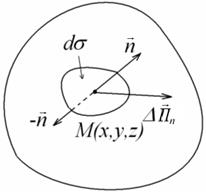
Рис. 1.6. К определению поверхностных сил

Между частицами сплошной среды обеих групп существует сцепление. Это сцепление, отражающее молекулярное взаимодействие в материалах хорошо соответствуют одной из основных гипотез физики, так называемой гипотезе «близкодействия». Согласно этой гипотезе силы молекулярного взаимодействия между отдельными частицами среды значительны только на весьма малых расстояниях, а с увеличением расстояния между ними резко убывают. Большинство реальных материалов (в том числе, вода, нефть, нефтепродукты и многие другие твердые и жидкие тела) удовлетворяют этой гипотезе. Поэтому сцепление двух групп частиц, разделенных площадкой 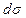, сводится к взаимодействию весьма тонких слоев сплошной среды, непосредственно примыкающих к площадке 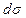с обеих ее сторон. В этом смысле говорят о поверхностном взаимодействии и о поверхностных силах.

Выбрав для данной площадки определенное направление нормали 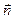, будем говорить о действии частиц, находящихся с той стороны площадки 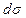, куда указывает вектор 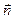(группа № 1), на частицы, находящиеся с другой её стороны (группу № 2). Будем считать, что это взаимодействие сводится к силе 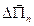, приложенной к элементарному поверхностному слою частиц группы №2. Индекс 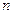указывает, что речь идет о взаимодействии частиц, разделенных площадкой с нормалью .

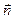Согласно третьему закону Ньютона о том, что "действие равно противодействию", сила 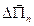, с которой частицы группы №2 (т.е. на площадке с нормалью 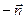), действуют на частицы группы №1, равна 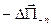по величине, но противоположны по знаку. Иными словами,

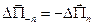. (1.19)