Закон сохранения массы. Уравнение неразрывности

Плотность 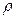и компоненты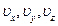 вектора скорости не могут быть произвольными величинами; сплошная среда должна двигаться так, чтобы выполнялся фундаментальный закон физики – закон сохранения массы. Как бы ни двигалась сплошная среда, но масса не должна ни появляться, ни исчезать.

Рассмотрим фиксированный 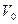объем пространства, взяв его в виде малого параллелепипеда с гранями, параллельными координатным плоскостям, и ребрами с длино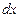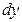й , и 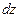(рис.1.4). Тогда одна из возможных формулировок закона сохранения массы сплошной среды состоит в следующем: изменение массы среды в рассматриваемом объеме за некоторый интервал времени 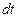должно равняться массе среды, втекающей за 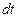в этот объем через его поверхность (вытекающую среду будем считать втекающей со знаком минус).

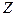
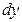
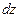
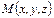
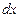
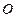
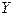
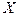
Рис. 1.4. К выводу закона сохранения массы

Масса 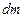сплошной среды в малом объеме 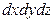равна 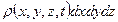, а ее изменение за время 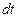выражается равенством

;

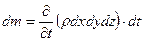Масса 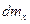сплошной среды, втекающей за время 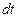в рассматриваемый параллелепипед через переднюю и заднюю боковые грани (т.е. грани, параллельные плоскости 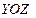на расстоянии 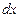друг от друга), может быть представлена равенством

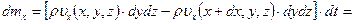
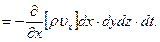
Аналогично, массы 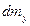и 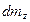втекающие через боковые грани параллелепипеда в направлении осе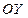й и 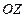, представляются, соответственно, выражениями:

,

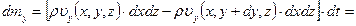
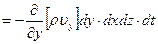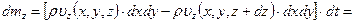
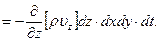
Отсюда следует, что суммарная масса 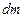сплошной среды, втекающей в параллелепипед через все шесть его граней, представляется выражением

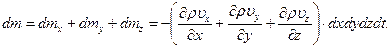
Сравнивая выражения для 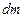, полученные в первом и втором пунктах, получаем дифференциальное уравнение

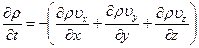
или

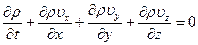, (1.14)

называемое уравнением неразрывности. Это уравнение, как следует из метода его получения, выражает закон сохранения массы движущейся среды.

Если в (1.14) выполнить дифференцирование по частям, то получим другую форму записи уравнения неразрывности:

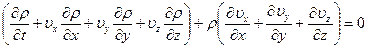
или, согласно (1.9):

.

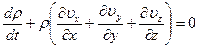Отсюда имеем:

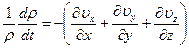. (1.15)

Сумма трех частных производных от компонент вектора скорости называют дивергенцией вектора 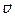и обозначают :

.

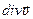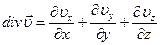Дивергенция вектора скорости показывает относительное изменение плотности сплошной среды. Итак:

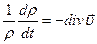(1.16)