Полная (индивидуальная) и частная (локальная)

Производные по времени

Поскольку большинство законов физики, в т.ч. механики и гидравлики, формулируется в виде соотношений между определяющими параметрами сплошной среды и скоростями их изменения, то необходимо более подробно рассмотреть такую характеристику, как производная по времени от определяющего параметра.

Согласно двум методам описания сплошной среды (методу Лагранжа и методу Эйлера), можно рассматривать два вида производных по времени: полную, относящуюся к изменения от времени параметра одной и той же частицы (и потому называемую индивидуальной), и частную, относящуюся к изменению от времени параметра среды в данной точке пространства (и потому называемую локальной или местной).

Полная (или индивидуальная) производная по времени, обозначаемая символом 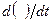, характеризует скорость изменения какой-либо характеристики сплошной среды у одной и той же движущейся частицы. Например, вдоль течения реки плывет плот с термометром. Этот плот измеряет температуру 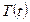одной и той же частицы воды, т.е. той, с которой он вместе движется. Вычисление на основе этих измерений 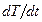дает полную производную по времени от температуры по времени. Также можно найти полные производные от других параметров движения.

Частная (или локальная) производная по времени, обозначаемая символом 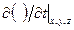, характеризует скорость изменения того же параметра по времени в фиксированной точке 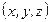пространства, и уже не относится к одной и той же частице среды. Вычисление 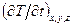в данной точке (створе) реки, дает локальную (местную) производную по времени от температуры воды.

Можно, сказать, что полная производная вычисляется при постоянных координатах 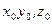, а локальная производная — при постоянных координатах .

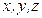Связь между полной и локальной производными по времени.Пусть 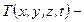какая-либо характеристика сплошной среды, например, ее температура, и пусть фиксированная частица среды за время 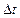переместилась из точки 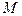с координатами 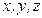в точку 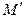с координатами 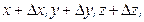где она имеет уже другую температуру 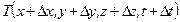. Полная производная 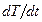от температуры частицы по времени определяется как предел отношения

.

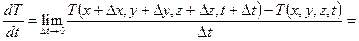
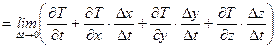Здесь использована формула конечных приращений:

+….,

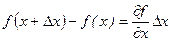известная из курса математического анализа (точками отмечены бесконечно малые высшего порядка по ).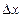

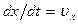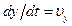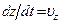Перейдя к пределу и заметив, что для фиксированной точки , и , получим

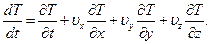(1.7)

В левой части равенства (1.7) стоит полная производная по времени, в то время как первое слагаемое правой части представляет локальную производную по времени. Локальная производная - это частная производная по времени от функции 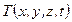, вычисленная при постоянных координатах 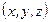. Формула (1.7) показывает, что скорость 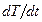изменения какого-либо параметра 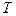по времени складывается из скорости изменения 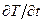этого параметра в данном месте пространства плюс добавочное слагаемое

.

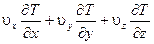Это добавочное слагаемое, называют конвективной составляющейполнойпроизводной по времени. Оновозникает в результате движения частицы. Очевидно, что в том случае, когда частица покоиться, т.е. 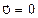, полная и локальная производные совпадают.