Основные определения сплошной среды
ОСНОВЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
Строение реальных сред и допущение о сплошности
Как известно, все тела представляют собой совокупности огромного числа различных атомов и молекул, которые находятся в постоянном тепловом движении и сложных условиях взаимодействия. В газе это взаимодействие связано, в основном, только со столкновениями; в жидкостях и твердых телах его природа носит гораздо более глубокий характер и имеет электромагнитную природу. Молекулярными процессами объясняются такие свойства реальных сред, как сжимаемость, вязкость, теплопроводность, упругость и др. Однако, сложность этих процессов чрезвычайно велика, а определяющие их силы не всегда известны. Поэтому такое, казалось бы, естественное рассмотрение движения среды путем изучения движения отдельных молекул, составляющих эту среду, совершенно неприемлемо. Больше того, ясно, что для решения практических задач совершенно несущественно знать движение каждой молекулы или атома, нужно лишь знание средних характеристик этого движения, например, движение центра масс некоторого «малого» объема вещества, содержащего, однако, достаточно много молекул.
Одним из общих методов изучения движения жидкости, газа и других деформируемых сред является метод механики сплошной среды, базирующийся на введении допущения о сплошности материала среды. Благодаря тому, что в любом существенном для макроскопических рассмотрений объеме содержится огромное число молекул, тело можно приближенно рассматривать как непрерывную среду, заполняющую пространство сплошным образом. Нефть, воду, воздух, металлы во многих случаях можно рассматривать как среду, непрерывно заполняющие некоторую область пространства.
Систему материальных точек, непрерывно заполняющую некоторую часть пространства, называют сплошной средой.
Замена реальной среды непрерывным континуумом представляет, конечно, идеализацию. Однако эта идеализация оказывается весьма удобной для использования математического аппарата непрерывных функций и, как показала практика, в огромном большинстве случаев вполне достаточна для описания реальных материалов.
Основные определения сплошной среды
Определим основные характеристики сплошной среды и, прежде всего, величину, описывающую распределение массы — плотность. Рассмотрим достаточно малый объем 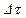 сплошной среды, содержащий точку
сплошной среды, содержащий точку 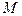 с координатами
с координатами 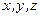 . Массу, заключенную в этом объеме, обозначим
. Массу, заключенную в этом объеме, обозначим 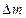 (рис. 1.1). Тогда отношение
(рис. 1.1). Тогда отношение 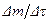 представляет собой среднюю плотность среды в объеме
представляет собой среднюю плотность среды в объеме 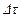 . Плотностью
. Плотностью 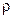 среды в точке М(
среды в точке М( 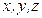 ) называется предел этого отношения при
) называется предел этого отношения при 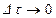 :
:
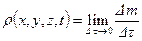 . (1.1)
. (1.1)
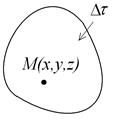
Рис.1.1. Произвольный объем сплошной среды
Если функция 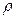 не зависит от пространственных координат
не зависит от пространственных координат 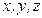 , т.е. плотность одинакова во всех точках среды, то такая среда называется однородной.
, т.е. плотность одинакова во всех точках среды, то такая среда называется однородной.
Масса сплошной среды, находящейся в малом объеме 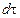 , представляется равенством
, представляется равенством 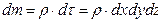 , а масса
, а масса 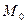 среды в замкнутом объеме
среды в замкнутом объеме 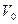 - формулой
- формулой
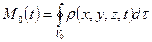 . (1.2)
. (1.2)
Наряду с плотностью 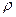 можно ввести удельный вессреды-
можно ввести удельный вессреды- 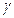 .Удельный вес определяется как предел отношения веса элемента среды
.Удельный вес определяется как предел отношения веса элемента среды 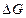 к величине
к величине 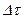 его объема:
его объема:
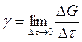 .
.
Очевидно, что 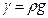 :
:
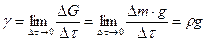 , (1.3)
, (1.3)
где g — ускорение силы тяжести.
Отметим размерности и единицы измерения для плотности удельного веса:
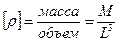 (в системе СИ -
(в системе СИ - 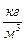 );
);
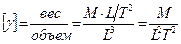 (в системе СИ -
(в системе СИ - 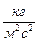 ).
).
Определим теперь скорость точек сплошной среды. Для того чтобы это сделать, необходимо указать, каким образом одну точку сплошной среды отличают от другой, т.е. индивидуализировать частицы сплошной среды.
Рассмотрим точки сплошной среды в некоторый начальный момент времени 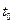 (рис. 1.2). Каждая из этих точек в начальный момент времени имеет определенные декартовые координаты
(рис. 1.2). Каждая из этих точек в начальный момент времени имеет определенные декартовые координаты 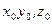 . В процессе движения положение каждой точки в пространстве изменяется, однако их начальные координаты
. В процессе движения положение каждой точки в пространстве изменяется, однако их начальные координаты 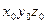 остаются неизменными. Таким образом, можно говорить о движении той частицы сплошной среды, которая в начальный момент времени имела координаты
остаются неизменными. Таким образом, можно говорить о движении той частицы сплошной среды, которая в начальный момент времени имела координаты 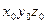 (рис. 1.3).
(рис. 1.3).
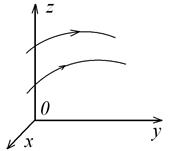 Рис. 1.2. Траектории
частиц сплошной среды
Рис. 1.2. Траектории
частиц сплошной среды
| 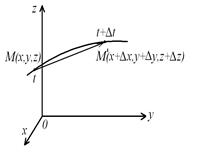 Рис. 1.3.Скорость частиц
сплошной среды
Рис. 1.3.Скорость частиц
сплошной среды
|
Отсюда следует, что закон движения сплошной среды можно задать тремя функциями:
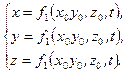 (1.4)
(1.4)
Если указаны координаты 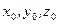 , то этим самым выделена частица среды, о которой идет речь, а формулы (1.4) определяют закон ее движения.
, то этим самым выделена частица среды, о которой идет речь, а формулы (1.4) определяют закон ее движения.
Пусть частица сплошной среды с начальными координатами 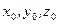 к моменту времени
к моменту времени 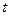 находилась в точке
находилась в точке 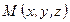 и за время
и за время 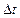 переместилась в точку
переместилась в точку 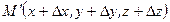 . Скоростью сплошной среды в момент времени
. Скоростью сплошной среды в момент времени 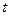 в точке с координатами
в точке с координатами 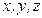 называется скорость той частицы, которая в этот момент времени совпадает с рассматриваемой точкой (рис. 1.3):
называется скорость той частицы, которая в этот момент времени совпадает с рассматриваемой точкой (рис. 1.3):

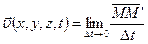 . (1.5)
. (1.5)
Равенство (1.5) является векторным, поэтому в проекциях на оси координат оно равносильно трем скалярным равенствам
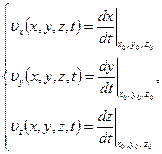 (1.6)
(1.6)
определяющим компоненты вектора скорости. Вертикальная черточка с буквами 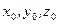 внизу указывает, что производные по времени берутся при постоянных координатах
внизу указывает, что производные по времени берутся при постоянных координатах 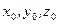 , т.е. для одной и той же частицы среды.
, т.е. для одной и той же частицы среды.
Дата добавления: 2016-05-16; просмотров: 1872;
