Теорема о представлении вектора напряжений на произвольной площадке через векторы напряжения на трех взаимно перпендикулярных (базисных) площадках
Оказывается, для того чтобы знать все векторы напряжений в точке 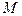 , т. е. знать вектор напряжения
, т. е. знать вектор напряжения 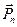 на любой площадке, проходящей через точку
на любой площадке, проходящей через точку 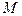 , достаточно знать всего лишь три вектора напряжения, в частности, на трех взаимно перпендикулярных площадках, проходящих через точку
, достаточно знать всего лишь три вектора напряжения, в частности, на трех взаимно перпендикулярных площадках, проходящих через точку 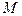 .
.
Рассмотрим произвольный прямоугольный тетраэдр МАВС, выделенный в сплошной среде, так что точка 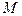 является его вершиной, а боковые грани МАВ, МВС, MСA параллельны координатным плоскостям, причем передняя грань
является его вершиной, а боковые грани МАВ, МВС, MСA параллельны координатным плоскостям, причем передняя грань 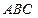 тетраэдра перпендикулярна единичному вектору
тетраэдра перпендикулярна единичному вектору 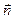 (рис. 1.9).
(рис. 1.9).
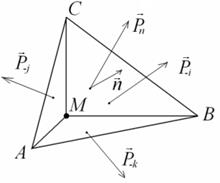
Рис. 1.9. К доказательству теоремы о напряжениях
Плоскости взаимно перпендикулярных граней, параллельные координатным плоскостям, имеют своими нормалями:
грань МАВ — вектор 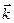 ,
,
грань МВС — вектор 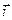 ,
,
грань МСА — вектор 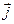 .
.
Часть сплошной среды, заключенная внутри тетраэдра, представляет собой систему материальных точек, поэтому к ней можно применить принцип Даламбера, состоящий в том, что сумма всех внешних сил, приложенных к этой системе, включая силу инерции 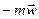 , равна нулю. Этот принцип эквивалентен второму закону Ньютона.
, равна нулю. Этот принцип эквивалентен второму закону Ньютона.
На сплошную среду, заключенную внутри тетраэдра, действуют следующие силы:
а) массовые 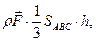 где
где 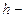 высота тетраэдра, опушенная из вершины
высота тетраэдра, опушенная из вершины 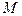 на грань АВС;
на грань АВС;
б) инерции 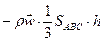 ;
;
в) поверхностные
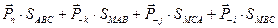 .
.
Здесь 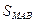 ,
, 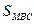 ,
, 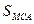 - площади граней тетраэдра.
- площади граней тетраэдра.
Поскольку 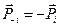 ,
, 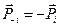 ,
, 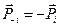 , см. (1.22), то сумма поверхностных сил равна
, см. (1.22), то сумма поверхностных сил равна
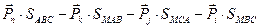 .
.
Боковые грани МАВ, МВС, MСA тетраэдра являются проекциями его основания 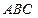 на координатные плоскости
на координатные плоскости 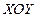 ,
, 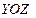 и
и 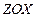 , соответственно, поэтому
, соответственно, поэтому
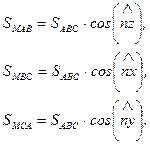
согласно известной теореме о том, что площадь прямоугольной проекции равна площади самой фигуры, умноженной на косинус угла проектирования. Отсюда следует, что сумму поверхностных сил можно представить в следующем виде:
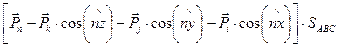 .
.
Согласно принципу Даламбера, сумма всех сил (включая силу инерции), действующих на сплошную среду, заключенную внутри тетраэдра, равна нулю, поэтому имеем:
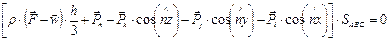 .
.
Последнее уравнение справедливо для тетраэдра произвольных размеров, поэтому можно устремить его высоту 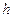 к нулю
к нулю 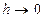 так, чтобы грань ABC, сохраняя свою ориентацию в пространстве, т.е. оставалась перпендикулярно первоначально выбранному вектору
так, чтобы грань ABC, сохраняя свою ориентацию в пространстве, т.е. оставалась перпендикулярно первоначально выбранному вектору 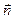 . При этом в силу непрерывности,
. При этом в силу непрерывности, 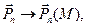
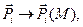
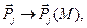 и
и 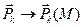 . В пределе имеем:
. В пределе имеем:
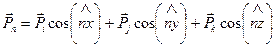 . (1.23)
. (1.23)
Формула (1.23) показывает, что вектор напряжения 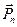 на любой площадке с нормалью
на любой площадке с нормалью 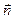 в точке
в точке 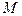 может быть представлен в виде линейной комбинации трех векторов
может быть представлен в виде линейной комбинации трех векторов 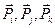 , выражающих векторы напряжений на трех взаимно перпендикулярных (базисных) площадках. Коэффициенты этого разложения равны косинусам углов между нормалью
, выражающих векторы напряжений на трех взаимно перпендикулярных (базисных) площадках. Коэффициенты этого разложения равны косинусам углов между нормалью 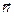 и координатными осями. В дальнейшем вектор
и координатными осями. В дальнейшем вектор 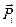 обозначается
обозначается 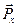 ,
, 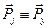 ,
, 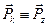 .
.
Дата добавления: 2016-05-16; просмотров: 856;
