Уравнения движения сплошной среды

В напряжениях

Перейдем теперь к выводу одного из основных уравнений механики сплошной среды — уравнения движения. Это уравнение представляет собой выражение 2-го закона Ньютона, применительно к сплошной среде. Согласно ему, сумма всех внешних сил, включая сил инерции, действующих на произвольно выделенный объем сплошной среды, равна нулю (или сумма внешних сил равна массе этого объема умноженной на ускорение его центра масс).

Рассмотрим произвольный объем сплошной среды, который для удобства возьмем в виде прямоугольного параллелепипеда с ребрами 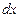, 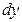и и 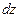гранями, перпендикулярными координатным осям (рис. 1.11).

Силы, действующие на среду в выделенном объеме, можно разделить на три группы:

а) внешние массовые силы:

;

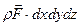б) силы инерции:

,

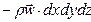в) поверхностные силы:

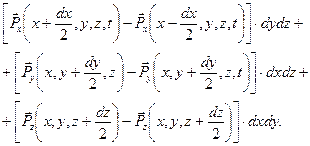
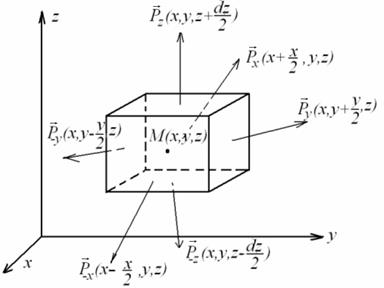
Рис. 1.11. К выводу уравнений движения сплошной среды

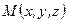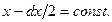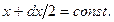Отметим, что точка представляет собой центр параллелепипеда; грани, перпендикулярные оси ОХ имеют уравнения и , соответственно, грани, перпендикулярные оси OY: 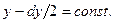, 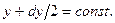и грани, перпендикулярные оси OZ: 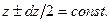Векторы напряжений берутся при соответствующих им аргументах.

Используя формулу конечных приращений, записанную, например, для вектора :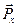

,

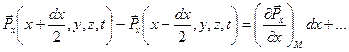где точки обозначают бесконечно малые второго порядка по 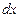, сумму поверхностных сил можно представить в следующем виде:

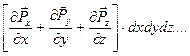
На основании 2-го закона Ньютона получаем уравнение

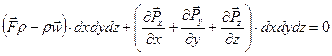
или после сокращения на 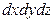- уравнение:

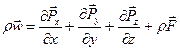. (1.29)

Это есть искомое уравнение движения, записанное в векторном виде.

Если использовать формулы (1.25), то векторное уравнение движения можно переписать в виде трех скалярных уравнений:

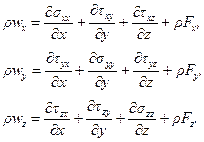(1.30)

Уравнения (1.30) называют уравнениями движения сплошной среды в напряжениях. Они применимы для описания любой сплошной среды: будь то вода, нефть, нефтепродукты, металл, смола или газ. Конкретные свойства среды, которая подлежит рассмотрению, будут учтены тогда, когда будет задана связь между напряжениями и деформациями, которые вызываются этими напряжениями. В записи этой связи появятся такие важные коэффициенты как вязкость, коэффициенты упругости и т.п.

Замечание о симметрии компонентов напряжений.Уравнение движения сплошной среды в напряжениях были получены путем составления баланса сил, действующих на произвольный объем среды. В теоретической механике известно, что при движении любой конечной частицы имеет место еще один закон - закон об изменении момента количества движения. Согласно этому закону, изменение момента количества движения равно сумме моментов всех внешних сил, приложенных к выделенной частице. Не производя выкладок, отметим, что такие уравнения приводят к равенству некоторых компонент напряжений, а именно:

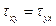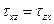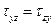, , . (1.31)

Эти равенства называют условиями симметрии касательных напряжений. Подробный вывод этих условий приводится в учебниках по механике сплошной среды [ ].