Компоненты напряжений. Касательные и нормальные

Напряжения

Каждый вектор напряжения можно разложить на две составляющие: нормальную (параллельную нормали к площадке) и тангенциальную (в плоскости площадки), рис. 1.10, так что

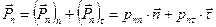. (1.24)

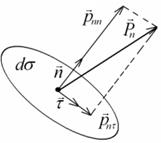
Рис. 1.10. Разложение вектора напряжения на нормальную и тангенциальную составляющие

Разложим на оставляющие по осям координат три базисные векторы напряжения 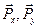и , и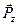меем:

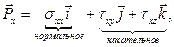
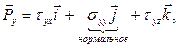(1.25)

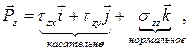
где единичные векторы вдоль координатных осей. Здесь 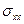читается так: проекция вектора напряжения 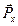на площадке, перпендикулярной оси ОХ, на ось OX; - проекция вектора напряжения 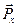на площадке, перпендикулярной оси ОХ, на ось OY и т. д. Девять коэффициентов разложения (1.25) называют компонентами напряжений; они являются основными характеристиками напряженного состояния в сплошной среде в точке .

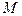Говорят, что вектор 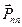представляет нормальное напряжение на рассматриваемой площадке, а вектор 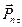— касательное напряжение на той же площадке.

Записанные в виде матрицы

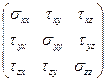, (1.26)

они полностью описывают напряженное состояние сплошной среды в точке 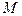. Зная компоненты напряжений в точке 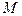, можно вычислить вектор напряжения 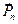на любой площадке с нормалью 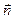. Используя формулу (1.23), получаем выражения для координат 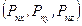вектора :

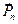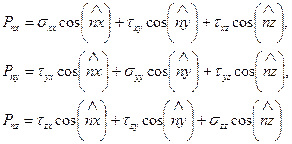(1.27)

или в матричном виде - как произведение матрицы (1.25) на единичный вектор :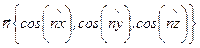

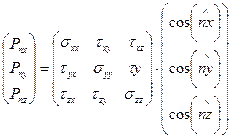. (1.28)