Уравнение парной регрессии

Если изучается связь между двумя переменными, причем их можно рассматривать как фактор и результат, т. е, вероятно наличие зависимости, то эту зависимость целесообразно представить в математическом виде. С этой целью подбирают функцию у = f(x), которая наилучшим образом соответствует исходным данным, иначе говоря, обеспечивает наилучшую аппроксимацию поля корреляции. При выборе типа функции руководствуются характером расположения точек на поле корреляции, а также содержанием изучаемой связи. Так, например, при изучении зависимости себестоимости единицы продукции (у) от объема производства (х) теоретический анализ показывает, что такая зависимость должна описываться уравнением гиперболы: 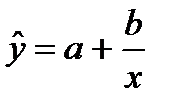, поскольку при увеличении объема производства себестоимость снижается до определенного предела, по достижении которого ее дальнейшего снижения не происходит. Однако расположение точек на поле корреляции может показать, что наилучшим образом исходным данным соответствует линейная функция .

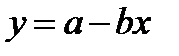Математически описание зависимости в среднем изменений переменной у от переменной х называется уравнением парной регрессии.

Чаще всего используется линейное уравнение парной регрессии:

,

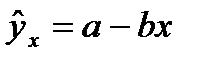где 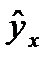— среднее значение результативного признака при определенном значении факторного признака х;

а — свободный член уравнения регрессии;

b — коэффициент регрессии, который показывает, на сколько единиц в среднем изменится результативный признак при изменении факторного признака на одну единицу его измерения.

При такой интерпретации коэффициента регрессии предполагается, что сила воздействия х на у постоянна при любых значениях х.

Знак при коэффициенте регрессии соответствует направлению зависимости у от х:

b > 0 — зависимость прямая;

b < 0 — зависимость обратная.

Если в исходных данных имеется нулевое значение х, то свободный член а показывает среднее значение у при х = 0.

Во всех остальных случаях а — доводка, обеспечивающая следующее равенство:

.

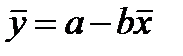В этом случае значение а не интерпретируется. Знак при свободном члене а зависит от соотношения между интенсивностью вариации (V) переменных х и у:

если V_y > V_x, то а < 0;

если V_y < V_x, то а > 0,

где а и b — параметры уравнения парной регрессии.

Если необходимо отразить нелинейность зависимости у от х, то могут быть использованы следующие уравнения регрессии:

,

,

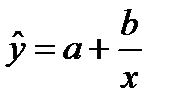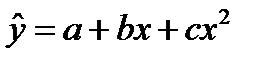
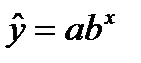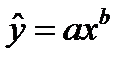
и т. д.

Выбираемые функции должны быть линейны по параметрам. Перечисленные регрессии приводятся к линейному виду (линеаризуются) путем замены переменных или логарифмирования.

Параметры линейного уравнения парной регрессии находятся методом наименьших квадратов (МНК). Исходное условие МНК формулируется следующим образом:

,

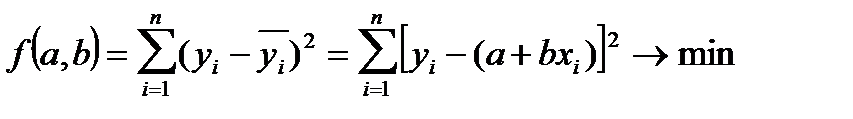т. е. должна быть обеспечена минимальность суммы квадратов отклонений фактических значений результативной переменной от ее теоретических значений, получаемых на основе уравнения регрессии.

Преобразуя полученные уравнения, получаем систему нормальных уравнений МНК для прямой:

,

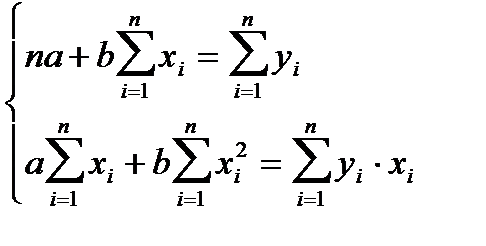Отсюда:

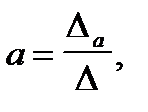
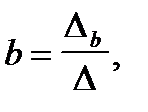
где — определитель системы;

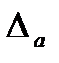— частный определитель, получаемый путем замены коэффициентов при а членами правой части системы уравнений;

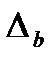— частный определитель, получаемый путем замены коэффициентов при b членами правой части системы уравнений.

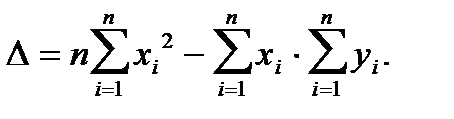
Тогда

.

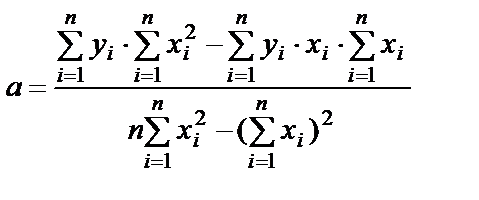
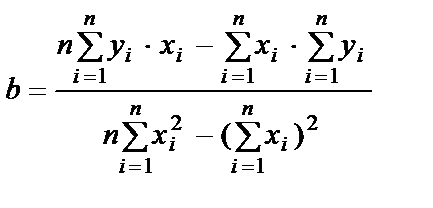Можно найти параметр а, разделив на п первое уравнение системы:

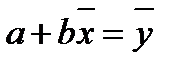, отсюда .

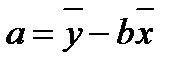Параметр b может быть выражен следующим образом:

.

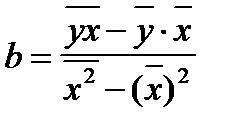Так как знаменатель этого выражения есть ни что иное как дисперсия переменной х, формула коэффициента регрессии b может быть записана следующим образом:

.

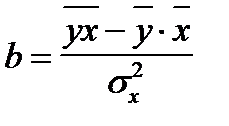Пример. По данным примера, рассмотренного в разд. 7.2, вычислим параметры уравнения линейной парной регрессии. Необходимые данные приведены в табл. 7.5.

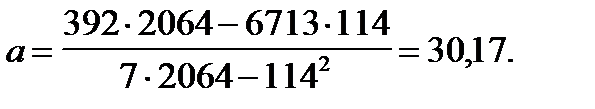
Таблица 7.5

Расчетная таблица

№ п/п
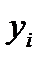
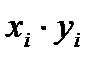
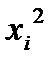
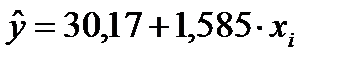
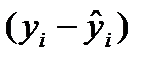
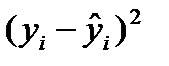
					46,02	-1,02	1,0404
					57,13	-7,13	50,8369
					53,86	1,14	1,2996
					69,84	0,16	0,0256
					60,31	1,69	2,8561
					61,90	3,10	9,6100
					42,84	2,16	4,6656
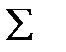
						X	70,3342

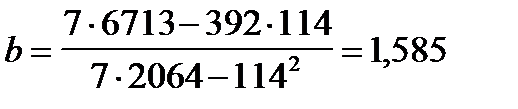руб/км.

Значение параметра а также можно получить на основе соотношения между 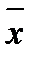и :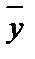

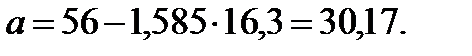
Получаем уравнение парной регрессии для описания зависимости цены от дальности доставки товара:

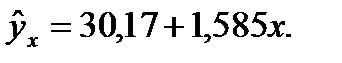
Параметр а в данном примере выполняет роль доводки до соотношения между средним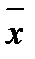и и 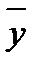. Конечно, можно предположить, что a — это та часть цены, которая не зависит от дальности перевозки. Параметр b (коэффициент регрессии) показывает, что с ростом дальности доставки на 1 км цена в среднем возрастает примерно на 1 руб. 59 коп.

Коэффициент регрессии можно найти на основе коэффициента корреляции. Поскольку

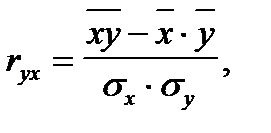
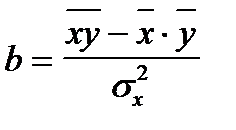
то .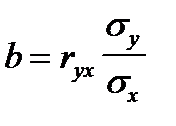

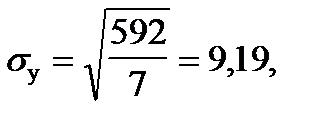
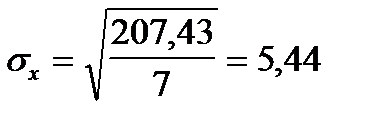
В нашем случае .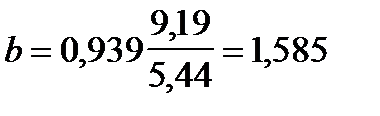

В отличие от коэффициента корреляции коэффициент регрессии является асимметричной характеристикой связи: он характеризует не просто связь между переменными, а зависимость изменения у от х, но не наоборот, т. е. .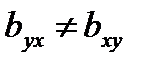

По уравнению 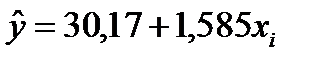рассчитаем теоретические значения цены 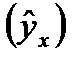. Результаты представлены в табл. 7.5. Значения 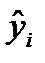, подтверждают, что найденная линия является наилучшей для аппроксимации исходных данных: .

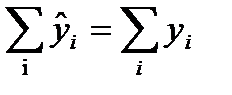Отклонения фактической цены от реальной невелики. Средняя ошибка аппроксимации определяется следующим образом:

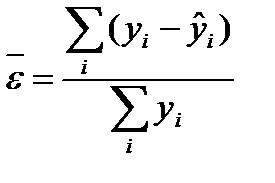
По данным примера = 4,16 %.

В последней графе табл. 7.5 показаны квадраты отклонений фактических значений ( 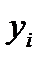) от расчетных ( ).

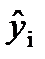Сумма 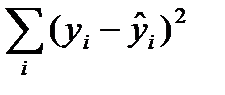является составляющей общей колеблемости у, которая в регрессионном анализе представлена следующим образом:

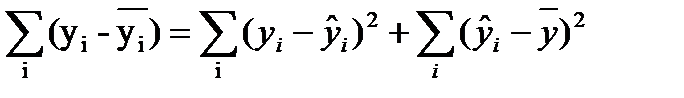
где 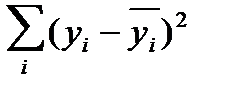— общая колеблемость;

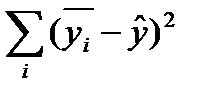— остаточная колеблемость;

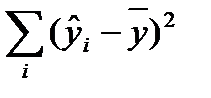—колеблемость у, объясненная уравнением регрессии.

Это разложение вариации зависимой переменной лежит в основе оценки качества полученного уравнения регрессии: чем большая часть вариации у объясняется регрессией, тем лучше качество регрессии, т. е. правильно выбран тип функции для отношения зависимости 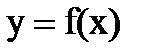, правильно выделена объясняющая переменная (признак-фактор) х.

Соотношение объясненной колеблемости и общей колеблемости у позволяет определить степень детерминации регрессией вариации у, т. е. найти коэффициент детерминации:

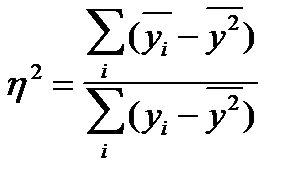
В нашем примере .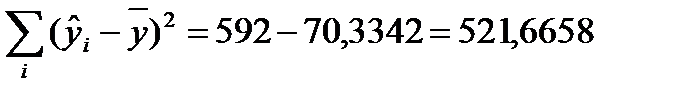

Отсюда 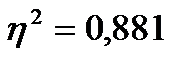или 88,1 %, что совпадает с ранее полученным значением коэффициента детерминации.