Понятие о статистической и корреляционной связи
В жизни все явления взаимосвязаны. Обычно нас интересуют непосредственные факторы, измерение их воздействия на результат, а также ранжирование факторов по интенсивности их влияния. Особенность связей в экономике и социальной сфере состоит в том, что их закономерный характер проявляется лишь в массе явлений — в среднем по совокупности. Всем известно, что затраты на рекламу, способствуя продвижению товару, приводят к увеличению выручки от продаж. Но по отношению к отдельному товару, отдельному продавцу эта закономерность может не подтвердиться. Она проявляется лишь в целом для многих товаров и фирм, и на основе обобщенных характеристик делается вывод об эффективности рекламы. Такого рода связи называют статистическими. Они проявляются в том, что при изменении значения фактора изменяется распределение результативного признака. Изменяются и условные средние значения результата (см. табл. 7.1).
Таблица 7.1
Проявление статистической и корреляционной связи
| Значения фактора | Количество единиц в группе | Распределение значений результата | Средние значения результата |
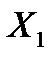
| k | y 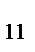 , y , y 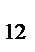 ... y ... y 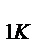
| 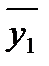
|
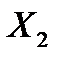
| т | y  , y , y  ... y ... y 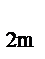
| 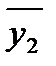
|
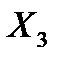
| Р | y 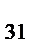 , y , y  ... y ... y 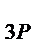
| 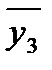
|
При статистической связи разным значениям одной переменной (фактора, х) соответствуют разные распределения другой переменной (результата, у).
Корреляционная связь — частный случай статистической связи, при котором разным значениям переменной соответствуют разные средние значения другой переменной.
Корреляционная связь предполагает, что изучаемые переменные имеют количественное выражение.
Статистическая связь — более широкое понятие, она не включает ограничений на уровень измерения переменных. Переменные, связь между которыми изучается, могут быть как количественными, так и неколичественными.
Возможность измерения связей во многом зависит от уровня измерения переменных. Основные сочетания переменных по уровням измерения и методы изучения связей представлены в табл. 7.2 (см. 3, с. 78).
Таблица 7.2
Методы изучения связей
| Шкала измерения переменной y | Шкала измерения переменной x | ||
| Номинальная | Порядковая | Интервальная | |
| Номинальная | Таблицы сопряженности, коэффициенты взаимной сопряженности | ||
| Порядковая | Ранговая корреляция | ||
| Интервальная | Аналитическая группировка, эмпирическое корреляционное отношение | Коэффициенты (индексы) корреляции, уравнения регрессии |
Из табл. 7.2 следует важный вывод: методы связей, предназначенные для переменных более низкого уровня измерения, могут использоваться и для изучения связей переменных более высоких уровней измерения (т.е. методы, которые применяются для изучения связей между номинальными переменными, могут использоваться для порядковых и интервальных переменных; это показано стрелками в табл. 7.2). Напротив, методы, разработанные для переменных более высокого уровня измерения (интервальных, т.е. количественных), не могут применяться для переменных более низкого уровня измерения.
Если изучается связь между двумя признаками, налицо парная корреляция. Если изучается связь между многими признаками — множественная корреляция.
Вопросы для самоконтроля
1. В чем заключается особенность связей в экономике и социальной сфере?
2. Какого рода связи называют статистическими?
3. Что такое корреляционная связь?
4. Могут ли использоваться методы связей, предназначенных для измерения переменных более низкого уровня измерения для изучения связей переменных более высоких уровней измерения?
Парная корреляция
Парная корреляция — это изучение корреляционной связи между двумя переменными.
Прежде всего, чтобы проверить, как проявляется связь между двумя переменными, нужно построить график-поле корреляции.
Поле корреляции — это поле точек, на котором каждая точка соответствует единице совокупности; ее координаты определяются значениями признаков х и у.
По характеру расположения точек на поле корреляции делают вывод о наличии или отсутствии связи, о характере связи (линейная или нелинейная, а если связь линейная, то прямая или обратная). На рис. 7.1 представлены основные типы корреляции между двумя переменными

| а) связь между x и y отсутствует | б) связь между x и y линейная обратная | в) связь прямая | г) связь нелинейная |
Рис. 7.1. Основные типы корреляции
В случае если точки корреляционного поля обнаруживают определенную направленность в своем расположении, можно говорить о наличии связи. При этом корреляционное поле можно оконтурить эллипсом (корреляционный эллипс).
Для того чтобы разобраться, как проявляется изучаемая связь у разных единиц, можно разделить корреляционный эллипс или поле корреляции на четыре области линиями 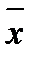 и
и 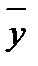 (см. рис. 7.2).
(см. рис. 7.2).
Пример. Изучается зависимость цены товара от дальности его перевозки по 7 фирмам. Данные представлены в табл. 7.3.
Таблица 7.3
Исходные данные
| Номер фирмы | Дальность перевозки, км (х) | Цена товара, руб. (у) |
| В среднем | 16,3 |
Поле корреляции представлено на рис. 7.2.

Рис. 7.2. Поле корреляции
В данном случае имеет место прямая связь между ценой товара и дальностью перевозки: три точки из семи попали в область (+ +), т. е. отклонения ( 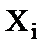 , -
, - 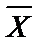 ) и (
) и ( 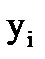 , -
, - 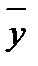 - положительны.
- положительны.
Отклонения от средних по одной и другой переменным лежат в основе измерения корреляционной связи. В случае линейной связи ее теснота измеряется с помощью коэффициента парной корреляции:
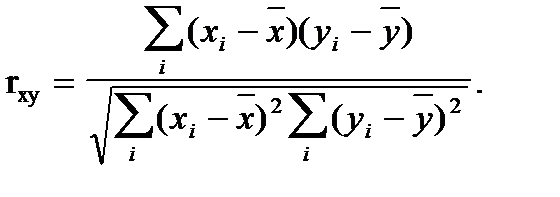
Если знаки отклонений от средних совпадают, то связь прямая ( 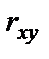 > 0), если знаки отклонений не совпадают, то связь обратная (
> 0), если знаки отклонений не совпадают, то связь обратная ( 
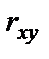 < 0). Разделив числитель и знаменатель на п (число наблюдений), получим:
< 0). Разделив числитель и знаменатель на п (число наблюдений), получим:
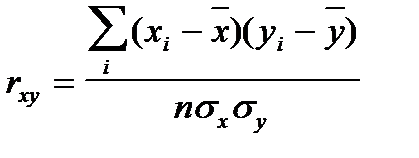
или
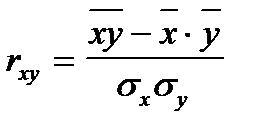
Коэффициент парной корреляции измеряется от -1 (случай полной обратной связи) до 1 (случай полной прямой связи). По абсолютной величине: 0 
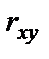
 1. Чем ближе значение
1. Чем ближе значение 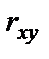 к единице, тем теснее связь, чем ближе значение
к единице, тем теснее связь, чем ближе значение 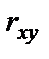 к нулю, тем слабее связь.
к нулю, тем слабее связь.
При | 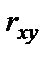 |<0,30 связь считается слабой, при |
|<0,30 связь считается слабой, при | 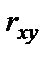 |= 0,3–0,7 — средней, при |
|= 0,3–0,7 — средней, при | 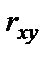 |> 0,7—сильной, или тесной.
|> 0,7—сильной, или тесной.
Коэффициент корреляции - симметричная мера связи, т. е. это мера взаимосвязи между х и у. Поэтому 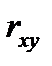 =
= 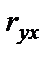 .
.
На основе данных табл. 7.3 рассчитаем коэффициент парной, корреляции между ценой товара и дальностью перевозки (табл. 7.4).
Данные табл. 7.4 показывают, что только в одном случае знаки отклонений от средних переменных х и у не совпадают.
Таблица 7.4
Расчетная таблица
| № п/п | 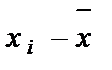
| 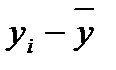
| 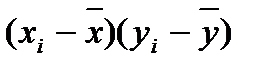
| 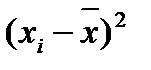
| 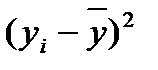
|
| -6,3 | -11 | 69,3 | 39,69 | ||
| 0,7 | -6 | -4,2 | 0,49 | ||
| -1,3 | -1 | 1,3 | 1,69 | ||
| 8,7 | 121,8 | 75,69 | |||
| 2,7 | 16,2 | 7,29 | |||
| 3,7 | 33,3 | 13,69 | |||
| -8,3 | -11 | 91,3 | 68,89 | ||
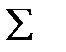
| X | X | 329,0 | 207,43 |
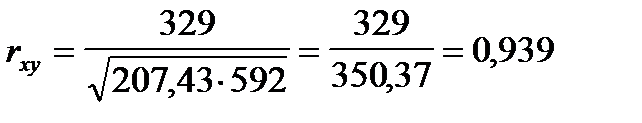
Полученное значение коэффициента корреляции показывает, что связь между ценой данного товара и дальностью его перевозки является очень тесной.
Интерпретация значения коэффициента корреляции зависит и от объема выборки. Существуют таблицы критических значений коэффициентов корреляции для разных объемов выборки (разного количества наблюдений). Так, при 3 наблюдениях можно утверждать наличие корреляционной связи лишь при очень высоких значениях коэффициента корреляции ( 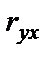
 0,997), а при 100 наблюдениях то же утверждение можно делать при
0,997), а при 100 наблюдениях то же утверждение можно делать при 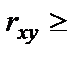 0,19.
0,19.
Квадрат коэффициента корреляции представляет собой коэффициент детерминации.
Коэффициент детерминации = 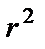 .
.
Коэффициент детерминации часто более предпочтителен для измерения связи, так как он может быть использован для измерения не только линейных, но и нелинейных связей. Коэффициент детерминации может быть выражен в процентах. В рассматриваемом примере 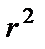 = 0,881, или, иначе говоря, на 88,1 % цена данного товара зависит от дальности его транспортировки. Конечно, нужно осторожно относиться к такого рода выводам и иметь в виду, что вряд ли полученное значение отражает в чистом виде зависимость цены от дальности перевозки. Здесь сказывается влияние и тех факторов, которые связаны с расстоянием доставки.
= 0,881, или, иначе говоря, на 88,1 % цена данного товара зависит от дальности его транспортировки. Конечно, нужно осторожно относиться к такого рода выводам и иметь в виду, что вряд ли полученное значение отражает в чистом виде зависимость цены от дальности перевозки. Здесь сказывается влияние и тех факторов, которые связаны с расстоянием доставки.
Коэффициент детерминации принимает значения в интервале [0, 1]. Чем ближе значение к 1, тем теснее связь, и наоборот.
Вопросы для самоконтроля
1. Что такое парная корреляция?
2. Что такое поле корреляции?
3. Назовите основные типы корреляции.
Дата добавления: 2016-05-16; просмотров: 1049;
