Понятие индекса. Виды индексов
Индекс — это показатель сравнения одного и того же явления. Каждый индекс включает данные за два периода: отчетный (сравниваемый, текущий) и базисный, который используется как база сравнения. Данные отчетного периода обозначаются подстрочным значком 1, базисного — 0.
Индекс, рассчитанный по отдельным единицам изучаемой совокупности, называется индивидуальным и обозначается i. Сводный (общий) индекс отражает изменение обобщенных величин по всей совокупности и обозначается символом I. Если при построении индекса исследуемый признак берется без учета связи его с другими признаками, то индекс называется простым и является оценкой только динамики признака. Индекс называется аналитическим, если изучаемый признак рассматривается не изолированно, а во взаимосвязи с другими признаками. Помимо обобщенной характеристики динамики непосредственно несоизмеримых явлений (синтетическая функция индексов), аналитические индексы выполняют аналитическую функцию, то есть позволяют измерить вклад отдельных факторов в совокупное изменение результата. Сводные аналитические индексы в зависимости от методов построения подразделяются на агрегатные и средневзвешенные из индивидуальных. Агрегатные индексы наряду с индексируемым признаком (признак, динамика которого изучается) содержат и признак-вес, который позволяет обобщить (соизмерить) разнородные элементы совокупности. Индексируемый признак при построении агрегатного индекса меняется: отчетный уровень сравнивается с базисным, признак-вес берется на неизменном фиксированном уровне либо базисного периода (по формуле Ласпейреса), либо отчетного периода (по формуле Пааше). Методы построения индексов различных явлений одинаковы. Рассмотрим их построение на примере следующей системы признаков:
- объем продаж( физический объем реализации) (q),
- цена (p),
- товарооборот или выручка от реализации (w = q·p).
Динамика признаков по отдельным элементам изучаемой совокупности может быть оценена с помощью индивидуальных индексов:

где q1, p1, w1 — oбъем продаж, цена и товарооборот по отдельным элементам совокупности в отчетном периоде,
q0, p0, w0 — объем продаж, цена и товарооборот в базисном периоде.
В целом по совокупности, состоящей из элементов, непосредственно несоизмеримых (различные виды продукции товарные группы и т. д.), изменение физического объема реализации и цен характеризуется с помощью агрегатных индексов, формулы построения которых приведены в табл. 6.1..
Таблица 6.1.
Агрегатные индексы
| Формула индексов | Название индексов | |
| Индекс физического объема и других первичных признаков | Индекс цен и других вторичных признаков | |
| По формуле Ласпейреса (по базисным весам) | 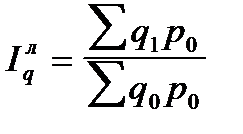
| 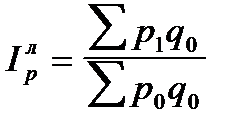
|
| По формуле Пааше (по отчетным весам) | 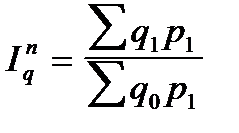
| 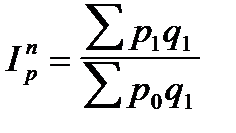
|
| Индекс Фишера | 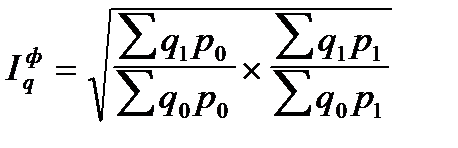
| 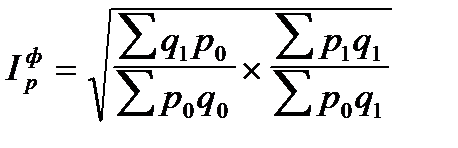
|
Сводный индекс товарооборота является простым и рассчитывается по формуле
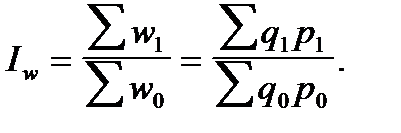
Индекс товарооборота может быть найден и через взаимосвязь индексов (мультипликативная модель индексов):
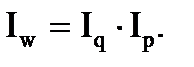
При этом для увязки индексов в систему веса в индексах первичных и вторичных признаков должны быть фиксированы на уровне разных периодов:
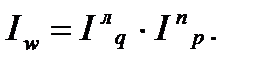
или
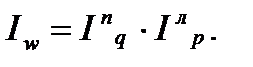 .
.
Отметим, что построение моделей взаимосвязанных индексов возможно лишь для сопоставимого круга элементов, то есть при неизменном ассортименте реализации отдельных товаров (товарных групп) в отчетном и базисном периодах.
Поскольку числитель и знаменатель агрегатных индексов имеют экономический смысл, в статистическом анализе нередко используются их разности. Так, например, разность числителя и знаменателя индекса товарооборота
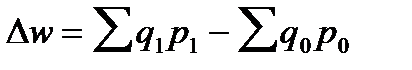
характеризуют абсолютный прирост (уменьшение) товарооборота в отчетном периоде по сравнению с базисным одновременно за счет:
а) изменения физического объема продаж,
б) изменения цен.
Измерить изолированное (элиминированное) влияние каждого из этих двух факторов можно через разность числителя и знаменателя соответствующих аналитических индексов.
Разность числителя и знаменателя индекса физического объема (по формуле Ласпейреса) показывает, как в абсолютном выражении изменился товарооборот за счет роста (сокращения) физического объема продаж:
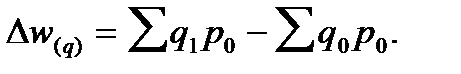
Разность числителя и знаменателя индекса цен (по формуле Пааше) означает абсолютный прирост (уменьшение) товарооборота в результате (снижения) цен.
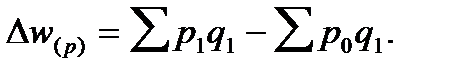
Абсолютное изменение за счет отдельных факторов в сумме дают общее абсолютное изменение результативного признака:
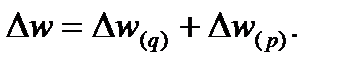
Эта же схема справедлива и для системы взаимосвязанных индексов, где индекс физического объема построен по отчетным весам (по формуле Пааше), а индекс цен — по базисным (по формуле Ласпейреса):
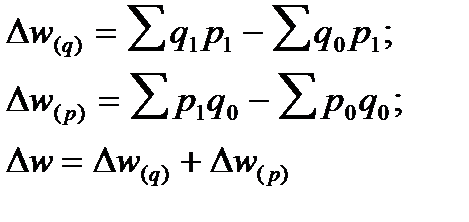
6.2. Индексный анализ изменения взвешенной средней:
индексы переменного и постоянного состава, индекс структуры
Индексный метод применяется в статистике также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. Эти задачи решаются с помощью системы взаимосвязанных индексов переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой соотношение средних величин какого-либо признака в отчетном и базисном периодах:
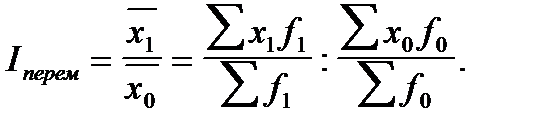
Как видно из формулы, индекс переменного состава характеризует изменение среднего уровня признака за счет влияния двух факторов:
1. изменения значений усредняемого признака (x) у отдельных единиц совокупности,
2. структурных изменений, под которыми понимается изменение доли отдельных единиц совокупности в общей их численности ( 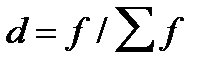 ).
).
Индекс постоянного (фиксированного) состава отражает изолированное действие первого фактора — показывает средний размер изменения изучаемого признака у отдельных единиц совокупности и строится как отношение средних взвешенных величин постоянного состава, т.е. с одними и теми же весами:
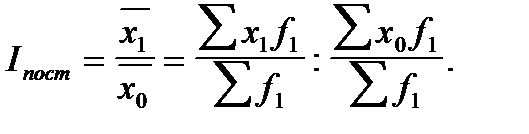
Индекс постоянного состава может быть рассчитан и в агрегатной форме:
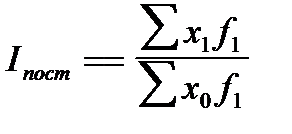
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака:
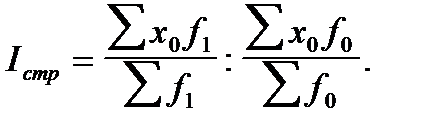
Индексы переменного, постоянного состава и структурных сдвигов увязываются в следующую систему:
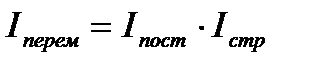
Если в индексах средних уровней в качестве весов используются удельные веса единиц совокупности в общей численности совокупности, т.е. показатели доли ( 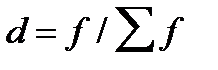 ) , то система индексов может быть записана в следующем виде:
) , то система индексов может быть записана в следующем виде:
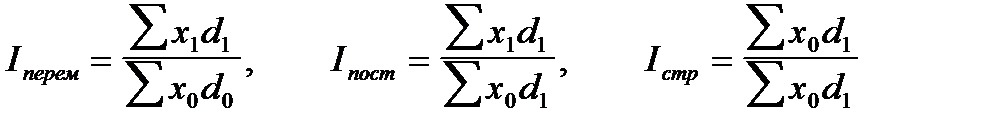
Система индексов переменного, постоянного состава и структурных сдвигов строится для изучения динамики среднего уровня цен, себестоимости, фондоотдачи, рентабельности, производительности труда, заработной платы и других вторичных признаков.
Помимо мультипликационной модели на основе индексов переменного, постоянного состава и структурных сдвигов может быть построено и аддитивное разложение, отражающее абсолютное изменение среднего уровня вторичного признака за счет отдельных факторов. Так, общий абсолютный прирост (уменьшение) среднего уровня признака в целом по совокупности находится как разность числителя и знаменателя индекса переменного состава:
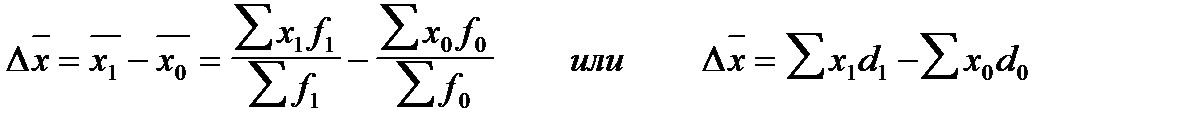
Абсолютный прирост (уменьшение) среднего уровня признака в целом по совокупности за счет изменения значений изучаемого признака у отдельных единиц совокупности и за счет структурных изменений рассчитывается соответственно как разность числителей и знаменателей индексов постоянного состава числителей и знаменателей индексов постоянного состава и структурных сдвигов:
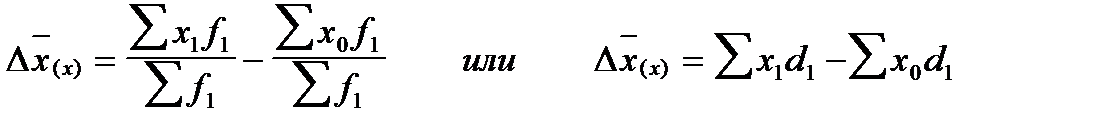
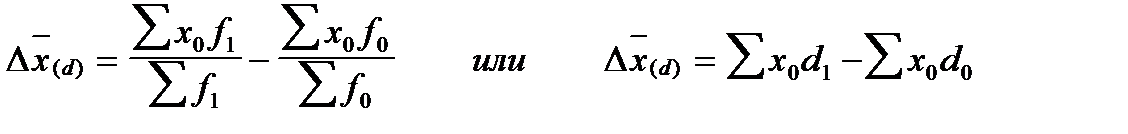
В общем виде аддитивное разложение имеет вид:
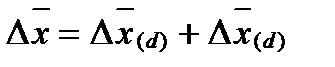
Пример. Имеются данные об объеме выпускаемой продукции и среднегодовой стоимости основных производственных фондов объединения за два года (табл. 6.2).
Таблица 6.2.
| Филиалы объединения | Объем продукции, млн. руб. | Среднегодовая стоимость основных производственных фондов, млн. руб. | ||
| базисный год | отчетный год | базисный год | отчетный год | |
| №1 | ||||
| №2 | ||||
| В целом по объединению |
Необходимо определить:
1. Уровни фондоотдачи в отдельных филиалах объединения в отчетном и базисном периодах,
2. Средний уровень фондоотдачи в целом по объединению в отчетном и базисном периодах.
3. Изменение среднего по объединению уровня фондоотдачи в отчетном периоде по сравнению с базисным, в том числе за счет:
А. Изменения уровня фондоотдачи в отдельных филиалах.
Б. структурных изменений.
4. Как изменился средний уровень фондоотдачи по объединению в абсолютном выражении за счет:
а) изменения фондоотдачи в филиалах,
б) структурных изменений,
в) совокупного действия двух факторов.
Уровень фондоотдачи (f) рассчитывается как отношение объема выпускаемой продукции (Q) к среднегодовой стоимости фондов (F).
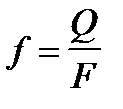
Вычислим фондоотдачу для каждого филиала в отчетном и базисном периодах:
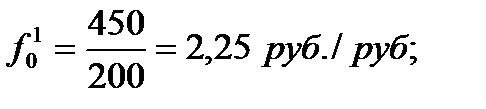
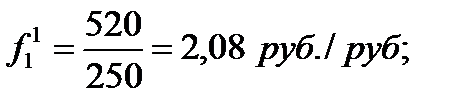
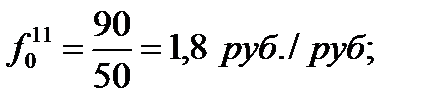
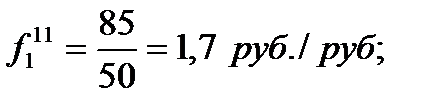
И в первом, и во втором филиале объединения фонды в отчетном периоде используются менее эффективно, чем в базисом. При этом в первом филиале сохраняется более высокий уровень фондоотдачи.
Средний по объединению уровень фондоотдачи в базисном и отчетном периоде составил:
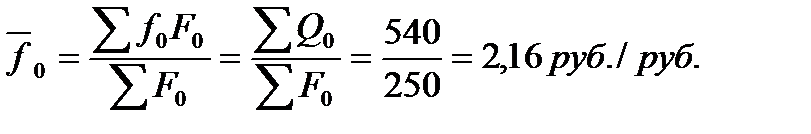
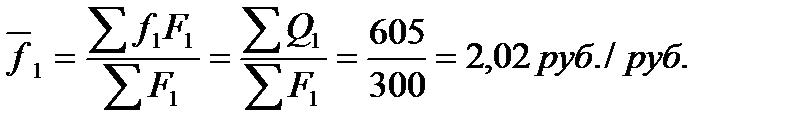
Динамику среднего по объединению уровня фондоотдачи характеризует индекс переменного состава
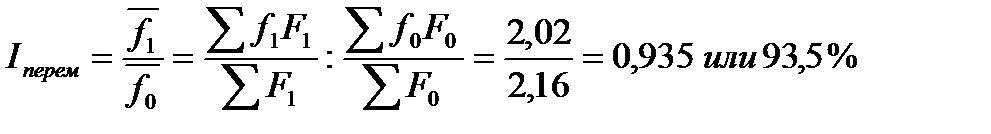 .
.
В целом по объединению в отчетном периоде по сравнению с базисным фондоотдача снизилась на 6,5 %. Изменение среднего уровня фондоотдачи в отдельных филиалах и структурных изменений в распределении фондов между филиалами.
Выявим раздельное влияние каждого из факторов:
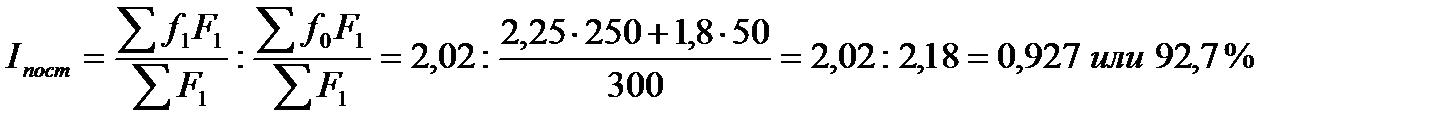
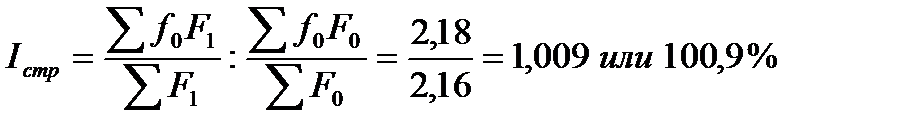
Таким образом, фондоотдача в среднем по филиалам объединения снизилась на 7,3 %, что привело к аналогичному снижению среднего уровня фондоотдачи в целом по объединению.
Структурные изменения, а именно увеличение доли фондов первого филиала, который характеризуется более эффективным уровнем их использования, обусловили рост среднего уровня фондоотдачи по объединению на 0,9 %.
Проверим увязку индексов в систему:
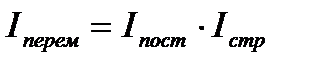
0,935 = 0,927·1,009
Для ответа на четвертый вопрос построим аддитивную модель на основе рассчитанных выше индексов переменного, постоянного состава и структурных сдвигов.
Абсолютное уменьшение среднего уровня фондоотдачи по объединению за счет изменения фондоотдачи в отдельных филиалах составит:
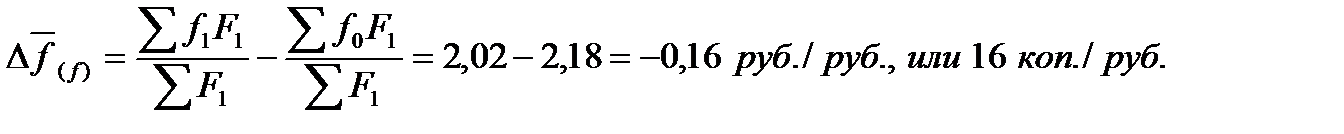
Абсолютный прирост фондоотдачи за счет структурных изменений:
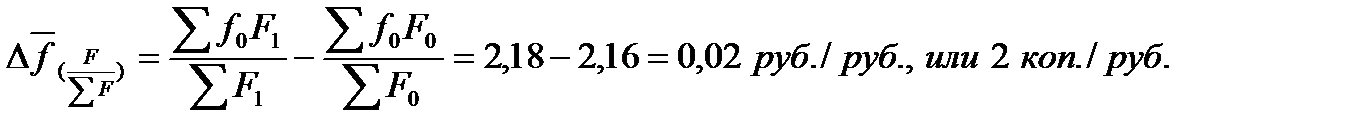
В целом изменение фондоотдачи за счет действия двух факторов можно определить двумя способами.
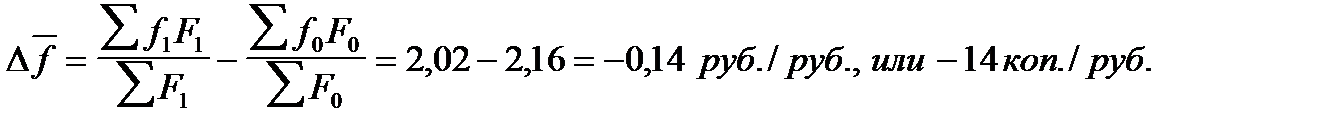
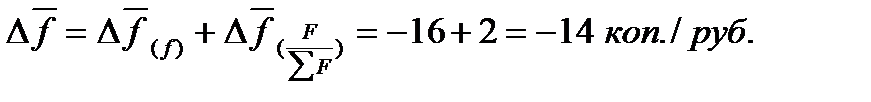
Таким образом, средняя по объединению фондоотдача уменьшилась за рассматриваемый период на 14 коп. с каждого рубля основных фондов, в том числе за счет снижения фондоотдачи в отдельных филиалах объединения средний уровень уменьшился на 16 коп. с рубля основных фондов, за счет структурных изменений (увеличение доли основных фондов первого филиала) средняя фондоотдача выросла на 2 коп. с рубля основных фондов.
Вопросы для самоконтроля
1. Что такое индекс?
2. Что такое индивидуальный индекс?
3. Чем отличается индивидуальный индекс от сводного?
Тесты к главе 6
1. Сводные аналитические индексы в зависимости от методов построения подразделяются на
a) индивидуальные,
b) агрегатные,
c) агрегатные и средневзвешенные из индивидуальных.
2. Методы построения индексов различных явлений:
a) одинаковы,
b) неодинаковы.
3. Построение моделей взаимосвязанных индексов возможно для:
a) сопоставимого круга элементов,
b) несопоставимого круга элементов.
4. Индекс структурных сдвигов характеризует:
a) соотношение средних величин какого-либо признака в отчетном или базисном периодах,
b) влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака.
Дата добавления: 2016-05-16; просмотров: 3158;
