Частная и множественная корреляция
Поскольку на изучаемый результативный признак влияет не один факторный признак, а множество, то возникает задача изолированного измерения тесноты связи результативного признака с каждым из признаков-факторов при элиминировании других признаков-факторов, а также задача измерения тесноты связи между результативными признаками и всеми признаками-факторами, включенными в анализ.
Коэффициенты парной корреляции называются коэффициентами нулевого порядка. На их основе можно рассчитать коэффициенты частной корреляции первого порядка, когда элиминируется корреляция с одной переменной. Например:
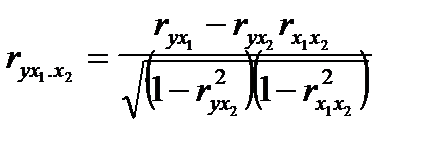
На основе коэффициентов частной корреляции первого порядка можно найти коэффициенты частной корреляции второго порядка:
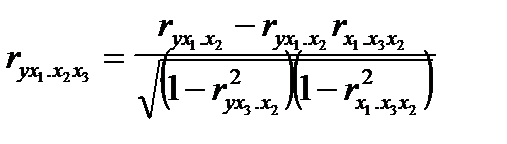
Таким образом, частная корреляция — это чистая (очищенная) корреляция между двумя переменными при погашении связи с другими переменными.
На основе коэффициентов частной корреляции второго порядка можно найти коэффициенты частной корреляции третьего порядка и т.д.
Коэффициент частной корреляции k-го порядка имеет вид:
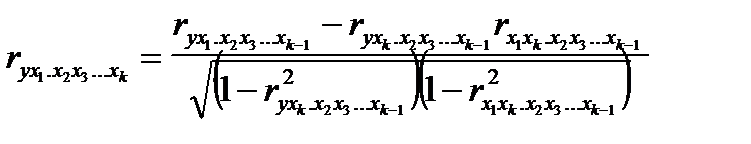
Коэффициенты частной корреляции принимают значения от -1 до 1, так как они являются мерами линейных связей. По абсолютной величине коэффициенты частной корреляции изменяются в интервале [0, 1].
На основе коэффициентов частной корреляции рассчитываются коэффициенты частной детерминации.
Коэффициент частной детерминации переменной xk — это доля дисперсии y, дополнительно объясняемой при включении переменной xk, в величине дисперсии y, не объясненной ранее включенными в анализ переменными.
Коэффициент частной детерминации обозначается как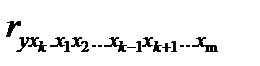 
.
Наиболее ясно суть коэффициентов частной детерминации выражает формула их расчета через коэффициенты множественной детерминации.
Коэффициент множественной детерминации показывает, какая часть дисперсии результативной переменной y объясняется за счет учтенных в анализе частных признаков. Этот показатель обозначается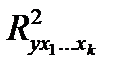 
и изменяется в интервале [0, 1].
,
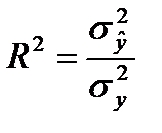где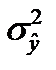 
— дисперсия переменной y, объясненная факторными переменными, включенными в анализ;
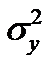— общая дисперсия переменной y.
Извлекая корень квадратный из R2, получаем коэффициент множественной (или совокупной) корреляции y со всеми учтенными переменными x1…xk.
Остановимся на определении коэффициента частной детерминации на основе коэффициентов множественной детерминации:
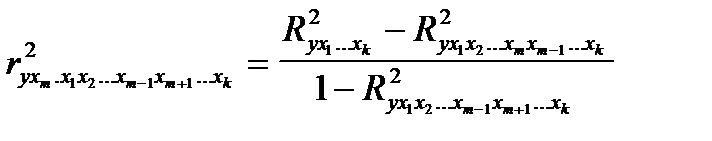
где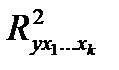 
— коэффициент множественной детерминации y при всех учтенных факторных переменных (включая xm);
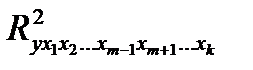— коэффициент множественной детерминации y без переменной xm.
Главное назначение коэффициентов частной детерминации — определить, имеет ли смысл введение в уравнение регрессии дополнительной объясняющей переменной или нет.
Назначение коэффициента множественной корреляции (или множественной детерминации) состоит в оценке качества уровня множественной регрессии: чем больше значение R, чем ближе оно к единице, тем лучше уравнение регрессии, тем надежнее результаты анализа или прогноза на его основе.
Вопросы для самоконтроля
1. Приведите пример статистической связи.
2. Что такое корреляционная связь?
3. Почему статистическая связь более широкое понятие, чем корреляционная связь?
4. Почему коэффициент детерминации часто более предпочтителен для измерения связи?
Тесты к главе 7
1. Корреляционная связь предполагает, что изучаемые переменные имеют:
a) количественное выражение,
b) качественное выражение.
2. Математическое описание зависимости в среднем изменений переменной y от переменной x называется:
a) уравнением множественной регрессии,
b) уравнением парной регрессии.
3. Статистическая связь
a) не включает ограничений на уровень измерения переменных,
b) включает ограничения на уровень переменных.
4. Коэффициент регрессии можно найти на основе коэффициента корреляции
a) верно,
b) неверно.
Экзаменационные вопросы к блоку 3
1. Понятие индекса. Виды индексов.
2. Индексный анализ изменения взвешенной средней: индексы переменного и постоянного состава.
3. Что характеризует индекс структурных сдвигов?
4. Для чего строится система переменного, постоянного состава и структурных сдвигов?
5. Что такое статистическая связь?
6. Что такое корреляционная связь?
7. Парная корреляция.
8. Частная и множественная корреляция. Каково назначение коэффициента множественной корреляции?
9. Уравнение парной регрессии.
Приложения
Ответы на тесты
Глава 1
1c; 2c; 3a; 4c.
Глава 2
1b; 2a; 3abc; 4a; 5b; 6c; 7c.
Глава 5
1a; 2b; 3a.
Глава 6
1c; 2a; 3b; 4b.
Глава 7
1a; 2b; 3a; 4a.
Контрольные работы
Номер варианта контрольной работы студент выбирает по последней цифре номера зачетной книжки.
Вариант 1
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 500 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Дайте определение частот и частостей вариационного ряда..
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 430 | 1 911 | 1 472 | 2 116 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 600 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 2
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 500 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Дайте определение гистограммы и кумуляты.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 450 | 1 911 | 1 472 | 2 116 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 700 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 600 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 3
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 600 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Дайте определение группировки.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 430 | 1 821 | 1 472 | 2 116 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 500 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 4
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 500 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Дайте определение моды и медианы.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 420 | 1 901 | 1 462 | 2 106 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 500 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 4. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 5
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 500 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Назовите задачи статистики.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 430 | 2 001 | 1 472 | 2 116 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 6500 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 6
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 500 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Дайте определение ряда динамики.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 430 | 1 911 | 1 562 | 2 116 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 600 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 7
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 500 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Каковы составляющие информационной базы статистики?
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 430 | 1 911 | 1 562 | 2 026 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 600 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 8
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 400 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Назовите задачи, присущие только социальной статистике.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 410 | 1 931 | 1 472 | 2 116 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 600 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 9
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 400 | |||
| 3. | 1 500 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Дайте определение статистического наблюдения.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 410 | 1 951 | 1 472 | 2 116 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 600 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Вариант 10
Задание № 1
В документе найти арифметическую и логическую рассогласованность.
| № | Заработная плата | Возраст | Общий стаж | Непрерывный стаж |
| 1. | ||||
| 2. | 1 500 | |||
| 3. | 1 400 | |||
| 4. | 2 000 | |||
| Итого | 5 200 |
Задание № 2
Дайте определение планомерности в статистике.
Задание № 3
Имеются данные о реализации изделий по кварталам
| I | II | III | IV |
| 2 430 | 2 001 | 1 562 | 2 196 |
Получить ряд динамики сопоставимых уровней реализации продукции по кварталам.
Задание № 4
Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
| № | Группы семей по размеру дохода | Число семей |
| 1. | до 500 | |
| 2. | 500–600 | |
| 3. | 600–700 | 1 800 |
| 4. | 700–800 | 2 600 |
| 5. | 800–900 | 2 300 |
| 6. | 900–1000 | 1 600 |
| 7. | свыше 1000 |
Определить моду и медиану.
Задание № 5
Выработка продукции в марте по цехам завода характеризуется показателями, представленными в таблице.
| № цеха | Численность рабочих, чел | Средняя выработка деталей за смену одним рабочим |
| 1. | ||
| 2. | ||
| 3. |
Вычислить выработку деталей на одного рабочего в среднем по заводу.
Учебный график студента по дисциплине «Статистика»
061000 «Государственное и муниципальное управление»
| № п/п | Наименование главы | Недели |
| 1. | Глава 1. Предмет, задачи и организация статистики | 1–2 |
| 2. | Глава 2. Методы статистики | 3–4 |
| 3. | Глава 3. Средние величины | 5–6 |
| 4. | Глава 4. Вариация | 7–8 |
| 5. | Глава 5. Динамика общественных явлений | 9–11 |
| 6. | Глава 6. Индексы | 12–14 |
| 7. | Глава 7. Статистический анализ связей | 15–18 |
| 8. | ИТОГО |
Дата добавления: 2016-05-16; просмотров: 1216;