Булева алгебра на выключателях и реле

Для того чтобы представить булевы переменные и операции над ними с помощью технических устройств (то, что сделал Клод Шеннон в своей диссертации), надо придумать схемы, которые воспроизводили бы эти операции согласно изложенным правилам. Для этого осталось сделать только один шаг: пусть наличие напряжения (высокий уровень напряжения) в некоторой точке цепи представляет собой логическую единицу, а отсутствие напряжения (низкий уровень) – логический ноль. В этом случае логика носит название «положительной». Если принять за единицу низкий уровень, а за ноль – высокий, логика будет «отрицательной». Как мы уже знаем, переход с положительной логики на отрицательную означает замену всех «И» на «ИЛИ» и наоборот. В дальнейшем, если это специально не оговорено, мы всегда будем иметь в виду положительную логику.

Самые простые варианты схем, реализующих базовые логические операции в этом случае, показаны на рис. 14.2.

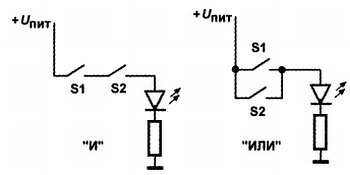
Рис. 14.2 . Схемы реализации логических функций на кнопочных выключателях

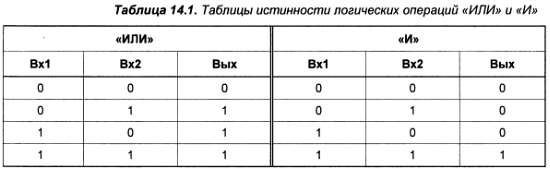
Здесь операции «И» и «ИЛИ» выполняются обычными кнопками без фиксации. Каждая из них соответствует одной логической переменной, которая принимает значение 1, если контакты замкнуты, и 0 – если разомкнуты. На выходе значению 0 соответствует погасший светодиод, значению 1 – горящий. Легко понять, что работать эти схемы будут именно так, как указано в таблицах для соответствующих логических операций. Для технических устройств правила соответствия входов и выхода называются «таблицами истинности» (или «таблицами состояния») и показаны в табл. 14.1.

Однако если разобраться поглубже, то придется констатировать, что настоящими входными логическими переменными для таких схем являются движения пальца, нажимающего на кнопку. В частности, операция «НЕ» здесь будет означать нажатие на кнопку с замкнутыми контактами, а каскадное соединение таких схем для реализации сложных выражений предполагает наличие человека, транслирующего выходной сигнал одной схемы (состояние светодиода) во входной другой схемы (состояние контактов). Логично поставить вместо такого человека, тупо выполняющего предопределенные действия, техническое устройство. И здесь помогут уже хорошо нам известные электромагнитные реле.

В схемах на рис. 14.3 как для входов, так и для выхода наличие напряжения соответствует логической 1, отсутствие его – логическому 0. (Можно для наглядности подключить к выходу светодиод или лампочку, но суть дела от этого не изменится.)

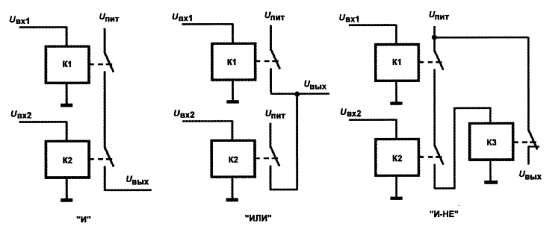
Рис. 14.3. Схемы реализации логических функций на реле.

Способ подачи входного сигнала не указан, т. к. предполагается, что источник входного напряжения может быть произвольным (разумеется, его мощность должна быть достаточной, чтобы заставить реле сработать) – в том числе и такая же схема на реле. Это иллюстрируется схемой на рис. 14.3 справа, где изображена схема составного элемента «И‑НЕ» на трех реле, представляющего собой объединение элемента «И» (такого же, как на рисунке слева) и элемента просто «НЕ» (инвертора), который есть не что иное, как одиночное реле с выходом через нормально замкнутые, а не нормально разомкнутые контакты.

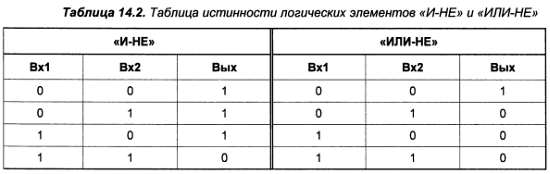
Таблица истинности для элемента «И‑НЕ», показанная в табл. 14.2, будет инверсией, представленной в табл. 14.1, таблицы истинности для элемента «И». Легко видеть, что она не совпадает с таблицей для «ИЛИ», как могло бы показаться на первый взгляд. Аналогично составляется элемент «ИЛИ‑НЕ» – из схемы «ИЛИ», показанной на рис». 14.3 посередине, и инвертора. Таблица истинности для него также представлена в табл. 14.2.

В большинстве современных применений логических микросхем используются именно элементы «И‑НЕ» и «ИЛИ‑НЕ», а не чистые «И» и «ИЛИ», – так удобнее и для разработчиков микросхем (где в качестве ключей служат транзисторы, которые инвертируют сигнал, см. далее), и для схемотехников. Для того чтобы было проще разбираться в логических схемах, не заучивая таблицы истинности, работу элементов можно запомнить следующим образом: элемент «И» дает единицу на выходе только, если на входах одновременно есть единица, элемент «ИЛИ» – если хотя бы на одном из входов единица. Возможно, вам еще проще будет запомнить так: элемент «ИЛИ» дает единицу на выходе, если на входах «хотя бы одна единица», а элемент «И» дает ноль на выходе, если на входах «хотя бы один ноль». Элементы с инверсией по выходу будут давать в тех же случаях обратные значения.

Интересно рассмотреть вопрос – а нельзя ли упростить схемы этих комбинированных элементов, исключив из них третье реле, выполняющее инверсию? В самом деле, большинство реле имеют перекидные контакты, так за чем же дело стало – меняем нормально разомкнутые контакты на нормально замкнутые, и все! Легко заметить, что такая замена не будет адекватной – мы инвертируем здесь не общий выход элемента, а выходы каждого реле в отдельности, что равносильно инвертированию входов. Если обратиться к правилам де Моргана, то мы увидим, что такое изменение схемы приведет к тому, что элемент «И» превратится в «ИЛИ‑НЕ», а «ИЛИ», соответственно, в «И‑НЕ». Я советую читателю посидеть над этими соображениями и вывести таблицы истинности самостоятельно, чтобы убедиться, что все сказанное – правда. Другое полезное упражнение состоит в том, чтобы попытаться самому построить трехвходовые элементы, соответствующие уравнениям А + В + С и А х В х С (они будет состоять из трех реле).

Тем, кто не разобрался как следует в этом по необходимости кратком изложении, среди прочих источников особенно порекомендую обратиться к [16] – книге, написанной очень простым и понятным языком, ориентированным на неподготовленного читателя, но вместе с тем излагающей предмет во всех подробностях.