То же самое, но на транзисторах и диодах

Ясно, что использование реле для построения логических схем – метод, мягко говоря, несовременный. Хотя в истории и отмечены случаи построения целых компьютеров на основе реле (к ним принадлежали, в частности, легендарные Mark‑I и Mark‑II Говарда Эйкена, запущенные в эксплуатацию в 1944 и 1947 гг., соответственно), но у них было слишком много недостатков: прежде всего, крайне низкие надежность и быстродействие, порядка 20–30 Гц (не килогерц и тем более не мегагерц, а именно герц). Конечно, по сравнению с электромеханическими ручными калькуляторами это было просто сказкой (типовое время операции сложения у Mark‑I составляло 0,3 с, т. е. в десятки и сотни раз превышало «быстродействие» человека с механическим калькулятором), и машины эти широко использовались на практике. Тем не менее, такое быстродействие казалось уже тогда недостаточным, потому довольно быстро перешли к использованию ламп, что позволило достичь порогов в десятки и сотни килогерц, а затем и транзисторов, с которыми частота работы возросла до единиц и десятков мегагерц.

* * *

Легенда о «баге»

С использованием реле в компьютерной технике связана легендарная история о возникновении термина «баг», как ошибки в программе. В буквальном переводе «bug» означает «жучок». В 1947 году между контактами одного из реле Mark‑II застряла мошка, вызвав неисправность. Когда мошку извлекли, молодая сотрудница Эйкена Грейс Хоппер (позднее – крупнейший авторитет в программировании и единственная в истории женщина‑адмирал флота США) приклеила ее между страницами лабораторного журнала с подписью: «первый случай выловленного бага». Страница эта сейчас хранится в музее Смитсоновского института.

* * *

Как же можно построить наши логические элементы на транзисторах? На рис. 14.4 показаны для примера схемы так называемой диодно‑транзисторной логики, которая широко использовалась в производстве гибридных микросхем (т. е. еще до изобретения Нойсом и Килби твердотельной микросхемы, см. главу 11 ).

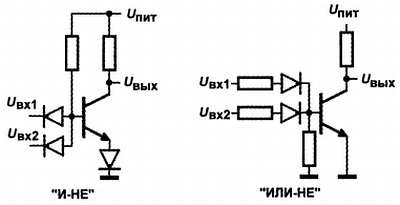
Рис. 14.4. Схемы реализации логических функций на диодах и транзисторах

В элементе «И‑НЕ» (слева) в нормальном состоянии транзистор открыт, и на выходе его логический ноль, так что подача логической единицы на входы ничего не изменит. А подача логического нуля хотя бы на один из входов приведет к тому, что соответствующий диод откроется и станет шунтировать переход база‑эмиттер, в результате чего транзистор закроется, и на выходе возникнет логическая единица, что соответствует функции «И‑НЕ». Диод в эмиттере нужен для обеспечения надежного запирания транзистора.

На схеме справа наоборот, транзистор в нормальном состоянии заперт, и на выходе логическая единица, а подача хотя бы одной логической единицы на входы откроет соответствующий диод и через него – транзистор, на выходе тогда установится логический ноль, что соответствует функции «ИЛИ‑НЕ». «Подпирающий» диод здесь не требуется, зато требуются токоограничивающие резисторы на входах.

Схему инверсии «НЕ» специально рисовать не имеет смысла, т. к. любой транзистор, включенный по схеме с общим эмиттером, как мы знаем из главы 6 , есть инвертор.

В случае необходимости обычные «И» и «ИЛИ» можно соорудить из этих схем, просто добавив к ним еще по одному транзисторному каскаду, но это снизит быстродействие и повысит потребление схемы. Отсюда понятно, почему разработчикам было удобнее проектировать микросхемы с инверсией, а не с «чистыми» булевыми функциями.

В этих схемах всплывает один вопрос, который для релейных схем был неактуален: с какого именно уровня напряжение считать логическим нулем, а с какого – единицей? В релейных схемах ноль – это полный разрыв цепи, а единица – полное ее замыкание. Здесь же не совсем так: на коллекторе открытого транзистора в левой схеме будет напряжение около 0,8–1 В, в то время как в правой – всего около 0,2–0,3 В. В то же время при закрытом транзисторе вроде бы напряжение логической единицы должно быть равно напряжению питания (токами утечки пренебрегаем). Однако оно тут же упадет, если мы нагрузим выход входом другой схемы типа «ИЛИ‑НЕ», поскольку там требуется обеспечить определенный ток базы.

Поэтому для транзисторов и микросхем задают не точный порог изменения с нуля на единицу, который, как мы видим, непостоянен, а пределы: ниже определенного значения считают выход находящимся в состоянии нуля (для схем на рис. 14.4 подойдет значение 1,2–1,5 В), а выше другого определенного значения (например, при питании 5 В пусть это будет 3,5 В) – в состоянии логической единицы. В промежутке схему считают находящейся в нерабочем режиме (в зоне неопределенности). При этом приходится ограничивать число устройств, подключаемых одновременно к выходу (или потребляемый по выходу ток). Для того чтобы расширить возможности таких схем, в серию одинаковых по типу применяемой схемотехники микросхем вводят специальные чипы буферов – т. е. усилителей мощности сигнала, которые никакой логической функции не осуществляют, а просто усиливают сигнал по току. Иногда такие буферы совмещают с функцией инверсии. Но прежде чем мы перейдем к логическим микросхемам, необходимо немного углубиться в теорию и терминологию и понять, что такое двоичные коды и как двоичная арифметика соотносится с булевой алгеброй.