На пороге цифрового века

Математическая логика и ее представление в технических устройствах

– Теперь давайте сочтем, сколько у нас всего. Портос?

– Тридцать экю.

– Арамис?

– Десять пистолей.

– У вас, Д'Артаньян?

– Двадцать пять.

– Сколько это всего? – спросил Атос.

– Четыреста семьдесят пять ливров! – сказал д'Артаньян, считавший, как Архимед.

А. Дюма . Три мушкетера

Все началось, конечно, с Аристотеля, который жил в IV веке до нашей эры. Когда читаешь вступление к любой популярной книге, посвященной чему угодно: от изящных искусств до биологии, химии, физики и математики, – возникает впечатление, что Аристотель был каким‑то сверхчеловеком. В самом деле, гении встречаются, но нельзя же быть гением настолько, чтобы разработать основы вообще всего, на чем зиждется современная цивилизация! Тем не менее, и авторы не врут, и Аристотель сверхчеловеком не был. Во‑первых, знаний было тогда накоплено еще не очень много, и обозреть их все – задача вполне посильная для человека острого ума и выдающихся способностей. Во‑вторых, Аристотель работал не один, его метод – коллективный мозговой штурм, это просто история донесла до нас фактически одно только его имя.

Но главное, пожалуй, в другом – древние рассматривали упомянутые нами дисциплины во взаимосвязи. Аристотель четко разделил только науку и ремесла («техно», по‑гречески), наука же делились на практические (этику и политику) и теоретические (физику и логику) дисциплины, но и они рассматривались как составные части единой науки. В чем древние, конечно, были более правы, чем мы, вынужденно поделившие области человеческой деятельности на множество автономных разделов.

Для нас важно, что главной составной частью науки считалась именно логика – искусство рассуждения. Вот она‑то и послужила той основой, из которой выросла цифровая техника и все многообразие информационных технологий, которые окружают нас теперь на каждом шагу.

Выдвинутые Аристотелем законы логики, которые с его же подачи стали идентифицироваться с законами мышления вообще, неоднократно пытались привести в математическую форму. Некто Луллий в XIII веке попытался даже механизировать процесс логических рассуждений, построив «Всеобщий решатель задач» (несомненно, это была первая попытка построения «думающей машины»). Формализацией логики занимался Лейбниц, искавший универсальный язык науки, и в конце концов все сошлось в двух работах английского математика Джорджа Буля, который жил и работал уже в середине XIX века. Любопытно название второй из этих работ – «Исследование законов мышления», первая же работа называлась поскромнее, но без «мышления» и тут не обошлось, – в названии фигурировало слово «рассуждения». То есть и сам Буль, и еще сто лет после него, до середины XX века, и все его предшественники в течение двух с большим лишком тысяч лет, прошедших со времен Аристотеля, – никто так и не усомнился, что в основе мышления лежит именно та логика, которая называется «аристотелевой». И лишь в XX веке, после работ Геделя и Тьюринга, и особенно в связи с благополучно провалившимися (как и у Луллия за 700 лет до того) попытками создания «искусственного интеллекта», до ученых, наконец, начало доходить, что мышление вовсе не имеет логической природы, а логика есть лишь удобный способ сделать свои рассуждения доступными окружающим.

Главное же следствие возникновения математической логики выявилось совсем не в исследованиях мышления, где оно виделось Лейбницу и Булю. Его обозначил в своей магистерской диссертации от 1940 года великий Клод Шеннон (рис. 14.1) – оказалось, что булевы законы в точности совпадают с принципами функционирования релейных электрических схем. Что самое поразительное – все компоненты, необходимые для моделирования законов логики с помощью электрических устройств (реле, выключатели), были известны еще до публикации Булем своих работ, но в течение еще почти ста лет никто не обращал на это внимания (Шеннон скромно утверждал, что случилось так, что до него просто никто не владел математикой и электротехникой одновременно). Не обратил на это внимание даже Чарльз Бэббидж, сконструировавший еще задолго до работ Буля механическую вычислительную («аналитическую») машину, – а ведь был знаком и с самим Булем, и с его работами!

Рис. 14.1. Клод Элвуд Шеннон (Claude Elwood Shannon), 1916–2001

_{ФотоLucent Technologies Inc /Bell Labs}

Основные операции алгебры Буля

Булева алгебра имеет дело с абстрактными логическими переменными. Эти переменные можно интерпретировать по‑разному, но интерпретацию мы пока отложим.

Вне зависимости от интерпретации, для логических переменных определены некоторые операции, подчиняющиеся определенным правилам. Базовые операции такие:

□ операция логического сложения двух операндов – операция объединения, операция «ИЛИ» («OR»), обозначается обычным знаком сложения;

□ операция логического умножения двух операндов – операция пересечения, операция «И» («AND»), мы будем обозначать ее крестиком, чтобы отличить от обычного умножения;

□ операция отрицания для одного операнда – операция «НЕ» («NOT»), обозначается черточкой над символом операнда.

В математике операция логического сложения (дизъюнкция) обозначается еще знаком v , а умножения (конъюнкция) – ^ . Кроме того, операция умножения часто обозначается знаком & , и это обозначение нам встретится, когда мы перейдем к микросхемам. Остальные операции могут быть записаны как сочетания этих трех основных.

Любая конкретная интерпретация булевых операндов – математическая или техническая – должна отвечать правилам булевой алгебры. Например, оказалось, что этим правилам отвечают множества (отсюда другие названия тех же операций: «пересечение» и «объединение»). Программисты имеют дело с логическими переменными 0 и 1, которые также есть одно из представлений булевых операндов.

Следует отчетливо понимать, что вне зависимости от интерпретации (включая и напряжения в релейных цепях по Шеннону), любые булевы объекты ведут себя одинаково: так, операция пересечения множеств совершенно адекватна операции «И» с логическими переменными или соответствующей манипуляции с выключателями в электрической сети.

В булевой алгебре многое совпадает с обычной – например, справедливы правила типа А + В = В + А или А + (В + С) = (А + В) + С), но для нас важны как раз отличия.

Вот они: А + А = А (а не 2А, как было бы в обычной алгебре), а также А х А = А (а не А²). Последнее уравнение в обычной алгебре, впрочем, имело бы решение, причем сразу два: 0 и 1. Таким путем обычно и переходят к интерпретации булевых операндов, как логических переменных, которые могут иметь только два состояния: 1 и 0 или «правда» (true ) и «ложь» (false ). В этом представлении мы действительно можем попробовать с помощью определенных ранее операций записывать некоторые высказывания в виде уравнений и вычислять их значения, что дает иллюзию формального воспроизведения процесса мышления. Но сначала надо определить, как и в обычной алгебре, правила, которым подчиняются операции, – т. е. таблицу логического сложения и таблицу логического умножения. Они таковы:

Операция отрицания «НЕ» меняет 1 на 0 и наоборот.

Примеры записи логических выражений обычно приводят для каких‑нибудь бытовых высказываний, но мы поступим нетрадиционно: приведем пример из области математики. Пусть высказывание состоит в следующем:«x меньше нуля или х больше 1 и у меньше 2». Как записать это высказывание? Введем следующие логические переменные: А = (х < 0); В = (х > 1);С = (у < 2). Как мы видим, все они могут принимать только два значения: «правда» (если условие выполняется) и «ложь» (если не выполняется). Обозначим значение всего выражения через D . Тогда высказывание записывается так:

D = (A +B ) xC (1)

Можно записать и так:

D = (A ИЛИ B ) И C

Или так:

D = (A ORB ) AND C

Или, наконец, так:

D = ((х < 0) OR (х > 1)) AND (у < 2)

Последняя запись хорошо знакома всем, кто изучал язык программирования Pascal . На языке С та же запись выглядит непонятнее:

D =((x < 0)||(x > 1))&&(y < 2)

* * *

Подробности

О великий и могучий язык С ! В нем самую простую вещь можно запутать до полной потери смысла. В нашем случае то же самое выражение можно было бы записать, как ((х < 0) | (х > 1)) & (у < 2), и ничего бы не изменилось. В этом языке (в отличие отPascal ) есть две разновидности логических операций: обычные («логическое И» &&, «логическое ИЛИ» ||) и поразрядные («поразрядное И» &, «поразрядное ИЛИ» |). Есть и, соответственно, «логическое НЕ» (!) и «поразрядное НЕ» (~). Термин «поразрядные» означает, что они применимы к многоразрядным двоичным числам. В результате их применения тоже получается многоразрядное двоичное число, необязательно ноль или единица, как в случае логических. Поскольку наши результаты операций сравнения содержат только один двоичный разряд (либо соблюдается, либо не соблюдается), то в данном случае логические и поразрядные операции оказываются идентичны, и можно писать и так, и так. А вот если в операциях участвуют обычные числа, то результат будет разный: «10&&7» равно «логической 1» (отличное от нуля значение всегда интерпретируется, как «правда»), тогда как «10&7» равно 2 (почему, будет рассказано далее). Как мы узнаем в главе 21 , эти особенности играют большую роль в программировании микроконтроллеров на языке С .

* * *

Пусть х = 0,5, у = 1. Чему будет равно D в этом случае? Очевидно, что выражение (А + В) примет значение «ложь» (0), поскольку х не удовлетворяет ни одному из условий А и В. Переменная С примет значение «правда» (1), но на результат это уже не повлияет, т. к. произведение 0 на 1, согласно таблице логического умножения, равно 0. То есть D в данном случае есть «ложь». Если же принять значение х = ‑0,5, оставив у равным 1, то D примет значение «правда».

Интересный оборот примут события, если вместо «OR» между А и В поставить «AND», – легко догадаться, что выражение в скобках тогда не будет «правдой» ни при каком значении х , поскольку условия «х меньше 0» и «х больше 1» взаимоисключающие. Потому результирующее условие D всегда будет принимать значение 0, т. е. «ложь». Но вот если мы изменим выражение следующим образом:

(2)

то есть инвертируем выражение в скобках с помощью операции «НЕ», то получим обратный результат: D всегда будет «правдой» (черточкой над символом или выражением как раз и изображается инверсия). Интересно, что тот же самый результат мы получим, если запишем выражение следующим образом:

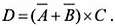
(3)

Это свойство выражается в так называемых правилах де Моргана (учителя Буля ):

Отметим, что из таблиц логического умножения и сложения вытекает еще одно любопытное следствие. Дело в том, что ассоциация значения «ложь» с нулем, а «правды» с единицей (положительная логика), есть действие вполне произвольное – ничто не мешает нам поступить наоборот (отрицательная логика). Такая замена приводит к тому, что все операции «ИЛИ» меняются на «И» и наоборот (рассмотрите таблицы внимательно). А вот операция «НЕ» к такой замене индифферентна – 0 меняется на 1 в любой логике.

Далее приведены несколько соотношений, которые вместе с правилами де Моргана помогают создавать и оптимизировать логические схемы. Некоторые из них очевидны, иные же – совсем нет.

Ассоциативный закон умножения:

A x B x C = (A xB ) x C = A x (B x C )

Ассоциативный закон сложения:

A + B + C = (A +B ) + C = A + (B + C )

Другие формулы: