Случайные ошибки измерения и их оценка

Я предполагаю, что читатель знаком с таким понятием, как вероятность. Если же нет – для знакомства настоятельно рекомендую книгу [12], которая есть переиздание труда от 1946 года. Расширить кругозор вам поможет и классический учебник [13], который отличает исключительная внятность изложения (автор его, известный математик Елена Сергеевна Вентцель, кроме научной и преподавательской деятельности, также писала художественную литературу под псевдонимом И. Грекова). Более приближен к инженерной практике другой учебник того же автора [14], а конкретные сведения о приложении методов математической статистики к задачам метрологии и обработки экспериментальных данных, в том числе с использованием компьютера, вы можете найти, например, в [15]. Мы же здесь остановимся на главном – расчете случайной погрешности.

В основе математической статистики лежит понятие о нормальном распределении. Не следует думать, что это нечто заумное – вся теория вероятностей и матстатистика, как прикладная дисциплина в особенности, основаны на здравом смысле в большей степени, чем какой‑либо другой раздел математики.

Не составляет исключения и нормальный закон распределения, который наглядно можно пояснить так. Представьте себе, что вы ждете автобус на остановке. Предположим, что автопарк работает честно, и надпись на табличке «интервал 15 мин» соответствует действительности. Пусть также известно, что предыдущий автобус отправился от остановки ровно в 10:00. Вопрос – во сколько отправится следующий?

Как бы идеально ни работал автопарк, совершенно ясно, что ровно в 10:15 следующий автобус отправится вряд ли. Пусть даже автобус выехал из парка по графику, но наверняка тут же был вынужден его нарушить из‑за аварии на перекрестке. Потом его задержал перебегающий дорогу школьник. Потом он простоял на остановке из‑за старушки с огромной клетчатой сумкой, которая застряла в дверях. Означает ли это, что автобус всегда только опаздывает? Отнюдь, у водителя есть план по выручке, и он заинтересован в том, чтобы двигаться побыстрее, потому он может кое‑где и опережать график, не гнушаясь иногда и нарушением правил движения. Поэтому событие, заключающееся в том, что автобус отправится в 10:15, имеет лишь определенную вероятность, не более.

Если поразмыслить, то станет ясно, что вероятность того, что следующий автобус отправится от остановки в определенный момент, зависит также от того, насколько точно мы определяем этот момент. Ясно, что вероятность отправления в промежутке от 10:10 до 10:20 гораздо выше, чем в промежутке от 10:14 до 10:16, а в промежутке от 10 до 11 часов оно, если не возникли какие‑то совсем уж форс‑мажорные обстоятельства, скорее всего, произойдет наверняка. Чем точнее мы определяем момент события, тем меньше вероятность того, что оно произойдет именно в этот момент, и в пределе вероятность того, что любое событие произойдет ровно в указанный момент времени, равна нулю.

Такое кажущееся противоречие (на которое, между прочим, обращал внимание еще великий отечественный математик Колмогоров) на практике разрешается стандартным для математики способом – мы принимаем за момент события некий малый интервал времени δt . Вероятность того, что событие произойдет в этом интервале, уже равна не нулю, а некоей конечной величине δР , а их отношение δР /δt при устремлении интервала времени к нулю для данного момента времени равна некоей величине р , именуемой плотностью распределения вероятностей . Такое определение совершенно аналогично определению плотности физического тела (в самом деле, масса исчезающе малого объема тела также стремится к нулю, но отношение массы к объему конечно), и потому многие понятия математической статистики имеют названия, заимствованные из соответствующих разделов физики.

Правильно сформулированный вопрос по поводу автобуса звучал бы так: каково распределение плотности вероятностей отправления автобуса во времени? Зная эту закономерность, мы можем всегда сказать, какова вероятность того, что автобус отправится в определенный промежуток времени.

Интуитивно форму кривой распределения плотности вероятностей определить несложно. Существует ли вероятность того, что конкретный автобус отправится, к примеру, позже 10:30 или, наоборот, даже раньше предыдущего автобуса? А почему нет – подобные ситуации в реальности представить себе очень легко. Однако ясно, что такая вероятность намного меньше, чем вероятность прихода «около 10:15». Чем дальше в обе стороны мы удаляемся от этого центрального наиболее вероятного срока, тем меньше плотность вероятности, пока она не станет практически равной нулю (то, что автобус задержится на сутки – событие невероятное, скорее всего, если такое случилось, вам уже будет не до автобусов). То есть распределение плотностей вероятностей должно иметь вид некоей колоколообразной кривой.

В теории вероятностей доказывается, что при некоторых предположениях относительно вероятности конкретных исходов нашего события эта кривая будет иметь совершенно определенный вид, который называется нормальным распределением вероятностей или распределением Гаусса. Вид кривой плотности нормального распределения и соответствующая формула показаны на рис. 13.6.

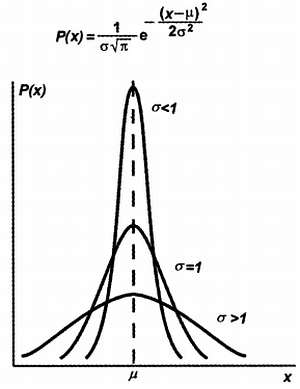
Рис. 13.6. Плотность нормального распределения вероятностей

Далее мы поясним смысл отдельных параметров в этой формуле, а пока ответим на вопрос: действительно ли реальные события, в частности интересующие нас ошибки измерений, всегда имеют нормальное распределение? Строгого ответа на этот вопрос в общем случае нет, и вот по какой причине. Математики имеют дело с абстракциями, считая, что мы уже имеем сколь угодно большой набор отдельных реализаций события (в случае с автобусом это была бы бесконечная таблица пар значений «плотность вероятности – время»). В реальной жизни такой ряд невозможно получить не только потому, что для этого потребовалось бы бесконечно долго стоять около остановки и отмечать моменты отправления, но и потому, что стройная картина непрерывного ряда реализаций одного события (прихода конкретного автобуса) будет в конце концов нарушена совершенно не относящимися к делу вещами: маршрут могут отменить, остановку перенести, автопарк обанкротится, не выдержав конкуренции с маршрутными такси… да мало ли что может произойти такого, что сделает бессмысленным само определение события.

Однако все же интуитивно понятно, что, пока автобус ходит, какое‑то, пусть теоретическое, распределение имеется. Такой идеальный бесконечный набор реализаций данного события носит название генеральной совокупности . Именно генеральная совокупность при некоторых условиях может иметь, в частности, нормальное распределение. В реальности же мы имеем дело с выборкой из этой генеральной совокупности. Причем одна из важнейших задач, решаемых в математической статистике, состоит в том, чтобы, имея на руках две разные выборки , доказать, что они принадлежат одной и той же генеральной совокупности – проще говоря, что перед нами есть реализации одного и того же события. Другая важнейшая для практики задача состоит в том, чтобы по выборке определить вид кривой распределения и ее параметры.

На свете сколько угодно случайных событий и процессов, имеющих распределение, совершенно отличное от нормального, однако считается (и доказывается с помощью так называемой центральной предельной теоремы), что в интересующей нас области ошибок измерений, при большом числе измерений и истинно случайном их характере, все распределения ошибок – нормальные. Предположение о большом числе измерений не слишком жесткое – реально достаточно полутора‑двух десятков измерений, чтобы все теоретические соотношения с большой степенью точности соблюдались на практике. А вот про истинную случайность ошибки каждого из измерений можно говорить с изрядной долей условности – неслучайными их может сделать одно только желание экспериментатора побыстрее закончить рабочий день. Но математика тут уже бессильна.

Полученные опытным путем характеристики распределения называются оценками параметров, и, естественно, они будут соответствовать «настоящим» значениям с некоторой долей вероятности – наша задача и состоит в том, чтобы определить интервал, в котором могут находиться отклонения оценок от «истинного» значения, и соответствующую ему вероятность. Но настало время все же пояснить – что же это за параметры?

В формуле на рис. 13.6 таких параметра два: величины μ и σ . Они называются моментами нормального распределения (аналогично моментам распределения масс в механике). Параметр μ называется математическим ожиданием (или моментом распределения первого порядка), а величина σ – средним квадратическим отклонением . Нередко употребляют его квадрат, обозначаемый как D или просто σ ², и носящий название дисперсии (или центрального момента второго порядка).

Математическое ожидание есть абсцисса максимума кривой нормального распределения (в нашем примере с автобусом – это время 10:15), а дисперсия, как видно из рис. 13.6, характеризует «размытие» кривой относительно этого максимума – чем больше дисперсия, тем положе кривая. Эти моменты имеют прозрачный физический смысл (вспомните аналогию с физическим распределением плотностей): математическое ожидание есть аналогия центра масс некоего тела, а дисперсия характеризует распределение масс относительно этого центра (хотя распределение плотности материи в физическом теле далеко от нормального распределения плотности вероятности).

Оценкой m_х математического ожидания μ служит хорошо знакомое нам со школы среднее арифметическое:

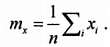
(2)

Здесь n – число измерений; i – текущий номер измерения (i = 1….,n ); x_i – значение измеряемой величины в i ‑м случае.

Оценка s² дисперсии σ ² вычисляется по формуле:

(3)

Оценка среднего квадратического отклонения, соответственно, будет:

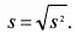
(4)

Здесь (x_i – m_х ) – отклонения конкретных измерений от ранее вычисленного среднего.

Следует особо обратить внимание, что сумму квадратов отклонений делить нужно именно на n – 1, а не на n , как может показаться на первый взгляд, иначе оценка получится неверной. Второе, на что следует обратить внимание, – разброс относительно среднего характеризует именно среднее квадратическое отклонение, вычисленное по формулам (3) и (4), а не среднее арифметическое отклонение, как рекомендуют в некоторых школьных справочниках, – последнее дает заниженную и смещенную оценку (не напоминает ли вам это аналогию со средним арифметическим и действующим значениями переменного напряжения из главы 4 ?).

* * *

Заметки на полях

Кроме математического ожидания, средние значения распределения вероятностей характеризуют еще величинами, называемыми модой и медианой. В случае нормального распределения все три величины совпадают, но в других случаях они могут оказаться полезными: мода есть абсцисса наивероятнейшего значения (т. е. максимума на кривой распределения, что полностью отвечает бытовому понятию о моде), а медиана выборки есть такая точка, что половина выборки лежит левее ее, а вторая половина – правее.

* * *

Этими формулами для расчета случайных погрешностей можно было бы ограничиться, если бы не один важный вопрос: оценки‑то мы получили, а вот в какой степени они отвечают действительности? Правильно сформулированный вопрос будет звучать так: какова вероятность того, что среднее арифметическое отклоняется от «истинного» значения (т. е. математического ожидания) не более чем на некоторою величину δ (например, на величину оценки среднего квадратического отклонения s )?

Величина δ носит название доверительного интервала , а соответствующая вероятность – доверительной вероятности (или надежности ). Обычно решают задачу, противоположную сформулированной, – задаются величиной надежности и вычисляют доверительный интервал δ . В технике принято задаваться величиной надежности 95 %, в очень уж серьезных случаях – 99 %. Простейшее правило для обычных измерений в этом случае таково: при условии достаточно большого числа измерений (практически, более 15–20) доверительной вероятности в 95 % соответствует доверительный интервал в 2s, а доверительной вероятности в 99 % – доверительный интервал в 3s . Это известное правило трех сигм, согласно которому за пределы утроенного квадратического отклонения не выйдет ни один результат измерения, но на практике это слишком жесткое требование. Если мы не поленимся провести не менее полутора десятков отдельных измерений величины ^х, то с чистой совестью можем записать, что результат будет равен:

х = m ± 2s .