Дискретизация сигналов по времени и квантование по уровню в системах цифрового управления

Дискретизация по времени является обязательным процессом в цифровых системах управления, что обусловлено дискретной природой самих ЭВМ. Регулируемый параметр объекта управления с помощью датчиков представляется обычно аналоговым сигналом, который с помощью аналого-цифрового преобразователя (АЦП) переводится в цифровую форму. Таким образом, непрерывно изменявшееся во времени состояние объекта управления преобразуется в последовательность чисел, которые обрабатываются ЭВМ. Под обработкой обычно понимается реализация закона регулирования. На выходе ЭВМ получается новая последовательность чисел, которая после преобразования в непрерывный сигнал подается на вход объекта управления. Преобразование в непрерывный сигнал производится с помощью цифро-аналоговых преобразователей (ЦАП). Процесс преобразования последовательности чисел в непрерывный сигнал называется восстановлением сигнала. Принцип работы ЭВМ в контуре управления заключается в том, что результаты обработки выдаются на выход в дискретные моменты времени t=0, T, 2T,…,

причем Т = t₁+t₂+t₃+t₄,

где t₁ – время опроса датчиков; t₂ – время выполнения программы; t₃ – время выдачи воздействия на объект управления; t₄ – резервное время.

В интервалах между решениями на выходе ЭВМ сохраняется то значение сигнала, которое было получено в начале интервала. В некоторых случаях производится также экстраполяция значений сигналов по линейному или квадратичному закону.

Для организации работы ЭВМ в реальном масштабе времени необходимо, чтобы Т не превышало Т_З, где Т_З – заданное время выдачи управляющих воздействий. Заданное время Т_З определяется динамическими свойствами объекта управления. Для определения Т_З используют аналитические методы теории автоматического регулирования, а также экспериментальные.

Дискретизация сигнала по времени означает простую замену этого сигнала его значениями на множестве дискретных точек. Дискретизация – это линейная операция. Моменты дискретизации в общем случае имеют постоянный период, и дискретизация называется периодической. Существуют и более сложные способы дискретизации. Такая дискретизация называется многочастотной и рассматривается как суперпозиция нескольких систем периодической дискретизации.

Кроме дискретизации по времени для получения цифровой формы производится квантование по уровню. Дискретизация сигналов по времени делает систему дискретной, а квантование по уровню – нелинейной. Необходимо помнить, что процессы дискретизации, квантования и восстановления сопровождаются возникновением методических погрешностей.

Рациональный выбор частоты дискретизации должен основываться на понимании ее влияния на качество систем управления. Вполне естественным является выбор максимальной частоты дискретизации исходя из полосы пропускания замкнутой системы. В этом случае выбор частоты дискретизации производится исходя из ширины полосы пропускания или, что то же самое, из времени разгона (времени регулирования) замкнутой системы. Разумные частоты дискретизации в 6-10 раз больше ширины полосы пропускания или от 2-х до 3-х дискретных отсчетов за время регулирования. Относительно низкие частоты дискретизации могут использоваться при управлении, так как динамические характеристики многих реальных объектов невелики и их постоянные времени обычно больше времени регулирования замкнутой системы.

Квантование сигналов по уровню представляет собой процесс выделения из точно измеренного значения сигнала x(t) дискретного уровня х(nТ), где Т – период дискретизации. Этот процесс можно представить как прохождение непрерывного импульса через элемент с многоступенчатой характеристикой, т.е. через m-разрядный АЦП. Количество ступеней определяется соотношением 2^m-1 и является количеством уровней квантования . Величина шага квантования h определяется соотношением

.

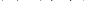
Максимальное значение абсолютной погрешности процесса квантования по уровню принимает значение h.

Нелинейность АЦП, действие которого основано на дискретизации по времени и квантовании по уровню, оказывает существенное влияние на динамические свойства систем. В некоторых случаях наблюдается возникновение периодических режимов и автоколебаний.

6. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ