Пример, построения прогнозной модели с мультипликативной компонентой

Для решения предыдущей задачи воспользуемся первым способом построения модели с мультипликативной компонентой. В общем случае его целесообразно использовать, если значение сезонной компоненты не является постоянной абсолютной величиной, а представляет определенную долю трендового значения.

1. Последовательность расчета значений сезонной компоненты существенно не отличается от рассмотренного в предыдущем примере. Также рассчитывается центрированная скользящая средняя, но оценка сезонной компоненты представляет собой не абсолютные отклонения, а относительные, которые принято называть индексами сезонности.

Таблица 21

Расчет коэффициентов сезонности

Период	Фактическое значение	Центрированная скользящая средняя	Алгоритм расчета	Индекс сезонности индивидуальный
1 квартал 2003
2 квартал 2003
3 квартал 2003			1791/2128	0,8418
4 квартал 2003			3332/2086	1,5972
1 квартал 2004			1658/2045	0,8108
2 квартал 2004			1486/1987	0,7477
3 квартал 2004			1617/1938	0,8346
4 квартал 2004			3045/1913	1,5915
1 квартал 2005
2 квартал 2005

2. Мы имеем оценки коэффициентов сезонности для каждого квартала. Для прогнозирования будущих тенденций нам необходимо оценить среднее влияние сезонного фактора для каждого сезона. С этой целью найдем среднее значение для каждого квартала. К сожалению, расчет по средней арифметической дает некоторую погрешность. Для устранения погрешности рассчитаем корректирующую составляющую, разделив сумму индексов сезонности на количество сезонов 3,9911/4=0,9978 и проведем корректировку (таблица 22).

Таблица 22

Расчет средних индексов сезонности.

Номер квартала	Индекс сезонности	Алгоритм расчета	Скорректированный индекс сезонности
1 квартал	0,8108	0,8108/0,9978	0,8126
2 квартал	0,7477	0,7477/0,9978	0,7494
3 квартал	0,8382	0,8382/0,9978	0,8401
4 квартал	1,5944	1,5944/0,9978	1,5979
Итого	3,9911

Значения индексов сезонности подтверждают наш вывод о наличие сезонных колебаний. В четвертом квартале объем продаж мяса значительно, в 1,5979 раз превышает среднеквартальный, а в остальные ниже среднеквартального.

3. Расчет тренда на основе полученных десезонализированных данных проводится традиционным методом прогнозной экстраполяции. Мы воспользуемся табличным редактором Excel, статистической функцией ЛИНЕЙН для определения параметров тренда. В результате нами получены параметры a= 2232, b=-43. Следовательно, уравнение модели тренда имеет следующий вид:

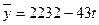
4. Оценим ошибку традиционными статистическими характеристиками дисперсия и среднеквадратическое отклонение. Дисперсия составит 43700, а среднеквадратическое отклонение 209,05

5. Прогнозирование по мультипликативной модели

Прогнозное значение объема продаж в 3 квартале 2005 г.

Y₁₁= (2232-43*11)*0,8401=1498 тыс. тонн

Прогнозное значение объема продаж в 4 квартале 2005 г.

Y₁₂= (2232-43*12)*1,5979=2782 тыс. тонн

<21 22 232425 26 27 >

Дата добавления: 2016-04-22; просмотров: 1069;