Построение прогнозной модели с аддитивной компонентой.
Последовательность этапов:
1. Построение и визуальный анализ графика сезонной волны.
2. Расчет значений сезонной компоненты. Согласно данному способу расчета сезонная компонента должна показать, на сколько единиц в среднем фактические значения в тот или иной сезон отличались от усредненных за период. Для выделения сезонной компоненты может быть использован метод скользящей средней.
3. Десезонализация данных, т.е. вычитание сезонной компоненты из
фактических значений.
4. Расчет тренда на основе полученных десезонализированных данных.
5. Оценка ошибки для оценки степени соответствия модели исходным данным. Расчет среднеквадратического отклонения.
6. Построение прогноза с учетом сезонных колебаний.
Пример
На основе информации о продаже мяса в ретроспективном периоде требуется составить прогноз продаж на будущий период (третий, четвертый квартал текущего года).
Таблица 14
Объем продаж мяса
| Период продаж | Объем продаж, тыс. тонн |
| 1 квартал 2003 | |
| 2 квартал 2003 | |
| 3 квартал 2003 | |
| 4 квартал 2003 | |
| 1 квартал 2004 | |
| 2 квартал 2004 | |
| 3 квартал 2004 | |
| 4 квартал 2004 | |
| 1 квартал 2005 | |
| 2 квартал 2005 |
1. Необходимо проанализировать множество исходных данных и установить, можно ли обнаружить тенденцию. С этой целью строится график сезонной волны.
График сезонной волны предназначен для визуальной оценки характера внутригодовых колебаний. По горизонтали отмечают номер временного интервала внутри года, а по вертикали фактические значения исследуемых характеристик. Если периоды роста или снижения исследуемой характеристики в одноименные периоды разных лет совпадают, то можно сделать вывод о сезонном характере внутригодовых колебаний. Если таких совпадений нет, то колебания внутри года вызваны другими причинами и данная методика для их анализа и прогнозирования не может быть применена.
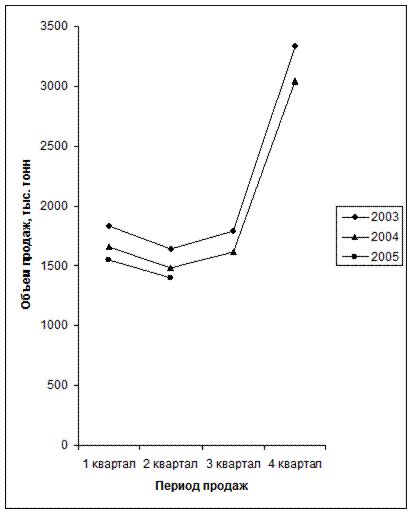
Рис.4. График сезонной волны
Как видно из графика сезонной волны, возможен убывающий тренд, содержащий сезонные колебания.
2. Расчет сезонной компоненты. Часто расчет сезонной компоненты осуществляют с использованием метода скользящей средней, который в нашем случае будет включать следующие процедуры:
2.1. Рассчитаем среднеквартальные объемы продаж для 2003. Среднеквартальный объем продаж в 2003 г. = (1834+1641+1791+3332)/4=2150
Полученное значение уже не содержит сезонной составляющей, поскольку представляет среднюю величину за год. Его можно использовать как значение тренда для середины года, т.е. точки, лежащей между вторым и третьим кварталом 2003 года. Последовательно передвигаясь вперед, рассчитаем средние значения для всех возможных исследуемых интервалов времени. Результаты расчетов оформим в таблицу 15.
Таблица 15
Расчет скользящей средней
| Период продаж | Алгоритм расчета | Период скольжения | Скользящая средняя за четыре квартала |
| 1 квартал 2003 | |||
| 2 квартал 2003 | |||
| 3 квартал 2003 | (1834+1641+1791+3332)/4 | 2-3 квартал | |
| 4 квартал 2003 | (1641+1791+3332+1658)/4 | 3-4 квартал | |
| 1 квартал 2004 | (1791+3332+1658+1486)/4 | 4-1 квартал | |
| 2 квартал 2004 | (3332+1658+1486+1617)/4 | 1-2 квартал | |
| 3 квартал 2004 | (1658+1486+1617+3045)/4 | 2-3 квартал | |
| 4 квартал 2004 | (1486+1617+3045+1546)/4 | 3-4 квартал | |
| 1 квартал 2005 | (1617+3045+1546+1404)/4 | 4-1 квартал | |
| 2 квартал 2005 |
2.2. Оценки значений тренда, полученные в результате расчета скользящих средних по четырем точкам, относятся к иным моментам времени, чем фактические данные. Например, первое значение 2150 тыс. тонн - это объем продаж за два последних месяца второго квартала и два первых месяца третьего квартала. Нам же необходимы десезонализированные средние значения, соответствующие тем же интервалам времени, что и фактические значения. Их позволяет найти процедура центрирования, заключающаяся в расчете средней арифметической для каждой пары значений (таблица 16).
Таблица 16
Расчет центрированной скользящей средней
| Период продаж | Алгоритм расчета | Центрированная скользящая средняя |
| 1 квартал 2003 | ||
| 2 квартал 2003 | ||
| 3 квартал 2003 | (2150+2106)/2 | |
| 4 квартал 2003 | (2106+2067)/2 | |
| 1 квартал 2004 | (2067+2023)/2 | |
| 2 квартал 2004 | (2023+1952)/2 | |
| 3 квартал 2004 | (1952+1924)/2 | |
| 4 квартал 2004 | (1924+1903)/2 | |
| 1 квартал 2005 | ||
| 2 квартал 2005 |
Аналогичная процедура может быть применена при определении сезонных отклонений за любой промежуток времени. Если количество сезонов нечетное, то рассчитанная скользящая средняя будет относиться к середине интервала и необходимость в центрировании отпадает. Например, при расчете колебаний по дням недели определяется скользящая средняя для 7 точек. Ее значение будет отнесено к середине недели, т.е. к четвергу.
2.3.Оценка сезонной компоненты может быть получена в результате сравнения центрированной скользящей средней и фактических значений временного ряда за каждый квартал (таблица 17).
Таблица 17
Оценка сезонной компоненты
| Период продаж | Фактический объем продаж | Центрированная скользящая средняя | Сезонная компонента |
| 1 квартал 2003 | |||
| 2 квартал 2003 | |||
| 3 квартал 2003 | -337 | ||
| 4 квартал 2003 | |||
| 1 квартал 2004 | -387 | ||
| 2 квартал 2004 | -501 | ||
| 3 квартал 2004 | -321 | ||
| 4 квартал 2004 | |||
| 1 квартал 2005 | |||
| 2 квартал 2005 |
2.4. Для каждого квартала мы имеем оценки сезонной компоненты. Для прогнозирования будущих тенденций нам необходимо оценить среднее влияние сезонного фактора для каждого сезона. С этой целью найдем среднее значение для каждого квартала. К сожалению, расчет по средней арифметической дает некоторую погрешность. Для устранения погрешности рассчитаем корректирующую составляющую, разделив сумму сезонных компонент на количество сезонов (таблица 18).
Таблица 18
Расчет средних значений сезонной компоненты.
| Номер квартала | Сезонная компонента | Скорректированная сезонная компонента |
| 1 квартал | -387 | -380 |
| 2 квартал | -501 | -494 |
| 3 квартал | -329 | -322 |
| 4 квартал | ||
| Итого | -28 |
Значения сезонной компоненты подтверждают наш вывод о наличие сезонных колебаний. В четвертом квартале объем продаж мяса значительно, на 1196 тыс. тонн превышает среднеквартальный, а в остальные ниже среднеквартального.
3. Десезонализация данных (таблица 19).
Таблица 19
Расчет десезонализированных данных
| Период продаж | Фактический объем продаж | Сезонная компонента | Десезонализированный показатель |
| 1 квартал 2003 | -380 | ||
| 2 квартал 2003 | -494 | ||
| 3 квартал 2003 | -322 | ||
| 4 квартал 2003 | |||
| 1 квартал 2004 | -380 | ||
| 2 квартал 2004 | -494 | ||
| 3 квартал 2004 | -322 | ||
| 4 квартал 2004 | |||
| 1 квартал 2005 | -380 | ||
| 2 квартал 2005 | -494 |
4.Десезонализированные значения можно использовать для построения модели основного тренда. Если по этим данным построить диаграмму, то можно сделать вывод о существовании линейного тренда. Поэтому для расчета параметров тренда воспользуемся табличным редактором Excel, выбрав из функций статистические, а в ней функцию "ЛИНЕЙН". В результате расчета получим следующие параметры тренда: а=2176, в=-38.
Следовательно, уравнение модели тренда имеет следующий вид:
 |
4. Оценка отклонения теоретических значений от фактических может быть осуществлена вычитанием из фактических значений значения, рассчитанного по уравнению тренда и сезонной компоненты (таблица 20)
Таблица 20
Расчет ошибки для модели с аддитивной компонентой
| Период | Фактическое значение | Сезонная компонента | Трендовое значение | Ошибка |
| 1 квартал 2003 | -380 | |||
| 2 квартал 2003 | -494 | |||
| 3 квартал 2003 | -322 | |||
| 4 квартал 2003 | ||||
| 1 квартал 2004 | -380 | |||
| 2 квартал 2004 | -494 | |||
| 3 квартал 2004 | -322 | |||
| 4 квартал 2004 | -23 | |||
| 1 квартал 2005 | -380 | |||
| 2 квартал 2005 | -494 |
Далее может быть использована любая из известных функций для оценки суммарной ошибки. Оценим ошибку традиционными статистическими характеристиками дисперсия и среднеквадратическое отклонение. Дисперсия составит 223049, а среднеквадратическое отклонение 472,28.
4.Прогнозирование по аддитивной модели
Прогнозное значение объема продаж в 3 квартале 2005 г.
Y11= 2176-38*11-322=1436 тыс. тонн
Прогнозное значение объема продаж в 4 квартале 2005 г.
Y12= 2176-38*12+1196=2906 тыс. тонн
Дата добавления: 2016-04-22; просмотров: 1760;
