Алгоритм Квайна построения сокращенной ДНФ.
1. Получить СДНФ функции f.
2. Провести все операции неполного склеивания.
3. Провести все операции поглощения.
Пример 1. Построим сокращенную ДНФ для функции, приведенной в таблице 3.1.
Таблица 3.1
| x y z t | 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 |
| f | 1 1 1 1 0 1 0 0 1 0 1 0 1 1 1 1 |
1. Строим СДНФ функции f:
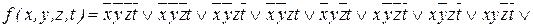
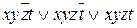 . Пронумеруем дизъюнктивные члены в полученной СДНФ в порядке от 1 до 11.
. Пронумеруем дизъюнктивные члены в полученной СДНФ в порядке от 1 до 11.
2. Проводим все операции неполного склеивания.
Первый этап склеивания в таблице 3.2.
После первого этапа склеиваний (и возможных поглощений) получаем, что 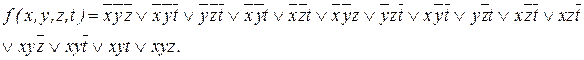
Пронумеруем дизъюнктивные члены в полученной ДНФ в порядке их следования от 1 до 15.
Второй этап склеиваний в таблице 3.3.
После второго этапа склеиваний и последующих поглощений получаем, что 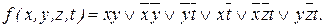 Это и будет сокращенной ДНФ для функции f, ибо дальнейшие склеивания невозможны.
Это и будет сокращенной ДНФ для функции f, ибо дальнейшие склеивания невозможны.
Таблица 3.2
| Слагаемые | Склеивание по | Результат |
| 1,2 | T | 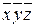
|
| 1,3 | Z | 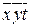
|
| 1,6 | X | 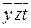
|
| 2,4 | Z | 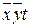
|
| 2,5 | Y | 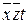
|
| 3,4 | T | 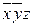
|
| 3,7 | X | 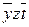
|
| 5,9 | X | 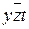
|
| 6,7 | Z | 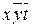
|
| 6,8 | Y | 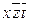
|
| 7,10 | Y | 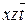
|
| 8,9 | T | 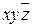
|
| 8,10 | Z | 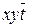
|
| 9,11 | Z | xyt |
| 10,11 | T | xyz |
Таблица 3.3
| Слагаемые | Склеивание по | Результат |
| 1, 6 | Z | 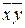
|
| 2, 4 | T | 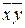
|
| 2, 8 | X | 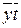
|
| 3, 7 | Z | 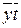
|
| 8, 13 | Y | x 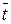
|
| 10, 11 | Z | x 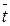
|
| 12, 15 | Z | xy |
| 13, 14 | T | xy |
Метод Блейка
Метод Блейка для построения сокращенной ДНФ из произвольной ДНФ состоит в применении правил обобщенного склеивания и поглощения. Подразумевается, что правила применяются слева направо. На первом этапе производится операция обобщенного склеивания до тех пор, пока это возможно. На втором производится операция поглощения.
Пример 2. Построить сокращенную ДНФ по ДНФ D функции f(x,y,z), где 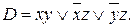
После первого этапа получаем: 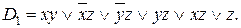
После второго этапа получаем сокращенную ДНФ: 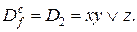
Дата добавления: 2016-03-27; просмотров: 1655;
