Наивные модели. Простые и скользящие средние
Эта группа объединяет простейшие методы прогнозирования, которые могут быть использованы при недостатке информации и времени на разработку прогноза. Прогноз, полученный данными методами, не будет отличаться высокой точностью, но будет давать некоторое представление о возможном значении исследуемого параметра в будущем.
Наивное прогнозирование основано на предположении, что предыдущее значение лучше всего предсказывает будущее. На практике предлагается несколько вариантов наивного прогнозирования.
1 вариант - прогнозное значение принимается равным предыдущему фактическому значению. Такой прогноз называют прогнозом без изменений.
ytпр =yt-1ф (9)
где ytпр -прогнозное значение в момент времени t,
yt-1ф - фактическое значение в момент времени t-1.
Этот вариант оценки будущего рекомендуется использовать, если в предыдущие периоды времени не происходило существенных изменений исследуемой характеристики или, если изменения носили разнонаправленный характер и взаимно погашались.
Например, в таблице 5 приведены данные о валовом сборе плодов и ягод в Алтайском крае.
Таблица 5
Динамика валового сбора плодов и ягод в Алтайском крае
| Валовый сбор, тыс.тн | 17,5 | 16,0 | 16,5 | 16,3 | 16,4 |
Самым простым методом разработки прогноза на 6 год будет прогноз без изменений. В этом случае прогнозное значение yпр6= 16,4 тыс. тн. Проверить качество прогноза можно, применив данный метод для оценки прогнозных значений в периоды со второго по пятый и сравнив их с фактическими значениями (таблица 6).
Таблица 6
Исходные данные и расчеты для оценки погрешности прогноза
| T | yt | ytпр | et | ׀et׀ | et2 | et/ yt | ׀et׀/ yt |
| 17,5 | - | - | - | - | |||
| 16,0 | 17,5 | -0,5 | 0,5 | 0,25 | -0,0312 | 0,0312 | |
| 16,5 | 16,0 | 0,5 | 0,5 | 0,25 | 0,0303 | 0,0303 | |
| 16,3 | 16,5 | -0,2 | 0,2 | 0,04 | -0,0123 | 0,0123 | |
| 16,4 | 16,3 | 0,1 | 0,1 | 0,01 | 0,0061 | 0,0061 | |
| сумма | -0,1 | 1,3 | 0,55 | -0,0071 | 0,0799 |
На основе данных таблицы рассчитаем известные нам характеристики погрешности прогноза:
σ= 0,37 тыс. тн, MAD = 0,325 тыс. тн, MPE = -0,18%, MAPE =2%.
2 вариант - наивный прогноз можно получить, учитывая последние абсолютные или относительные изменения показателей. Применяется, если значение фактических величин изменяются во времени.
Например, численность занятых в экономике России составила в 2003 г. 67152 тыс. чел., а в 2004 г. -67134 тыс. чел., т.е. за один год сократилась на 18 тысяч человек или на 0,027%.
Учитывая абсолютное изменение показателя, прогнозная численность занятых в экономике России составит в 2005 г 67116 тыс. чел.= (67134-18).
Учитывая относительное изменение показателя (сокращение на 0,027%), прогнозная численность занятых в экономике России составит в 2005 г 67116 тыс. чел.= 67134*(100-99,973)/100.
Методы прогнозирования, основанные на усреднении, применяются, когда оперативно нужно обновлять прогнозы для реестров, содержащих большое количество исходных данных. Ограниченность их применения заключается в том, что они позволяют получить только одно прогнозное значение.
Методы простых средних. Прогнозное значение рассчитывается на основе обобщенных средних характеристик временного ряда в ретроспективном периоде. Эти характеристики представляют собой выражение динамики за весь период одним средним числом. К средним характеристикам динамики относятся:
· средний уровень ряда или средняя хронологическая;
· средний абсолютный прирост;
· средний темп роста;
· средний темп прироста.
Средний уровень ряда показывает, какая средняя величина уровня характерна для всего анализируемого периода. К расчету среднего уровня прибегают для рядов, состояние или изменение которых стабильно в течение большого периода времени и рядов с колеблющимися уровнями в короткие промежутки времени. Показатель рассчитывается различно для интервальных и моментных рядов.
Для интервального ряда сумма значений фактических показателей временного ряда делится на число показателей (10):
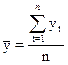 (10)
(10)
Для моментного ряда расчет осуществляется по формуле 11. Следует учесть, что значение первого и последнего показателей временного ряда берутся в половинном размере, поэтому в знаменателе количество показателей уменьшается на единицу.
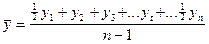
 (11)
(11)





 Средний абсолютный прирост ряда показывает скорость развития явления и рассчитывается по формуле 12.
Средний абсолютный прирост ряда показывает скорость развития явления и рассчитывается по формуле 12.
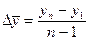 (12),
(12), 








где у 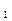 - последний зарегистрированный показатель временного ряда,
- последний зарегистрированный показатель временного ряда,
у 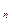 - последний зарегистрированный показатель временного ряда,
- последний зарегистрированный показатель временного ряда,
n - число показателей временного ряда.
Средний темп ростаможет быть рассчитан по формуле средней геометрической, при сравнении последнего показателя временного ряда с первым расчет осуществляется по формуле 13 .
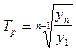 (13)
(13)
Средний темп прироста определяется по формуле 14.
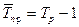 (14)
(14)
Следует учесть, что средние показатели можно использовать только для равномерно меняющихся явлений.
Метод простого скользящего среднего. Прогноз строится с учетом не всех наблюдений, а определенного количества последних наблюдений. Как только новое наблюдение становится доступным, оно включается в расчетную формулу, а наиболее старое исключается. Скользящее среднее порядка k - это среднее значение k последовательных наблюдений. (15)
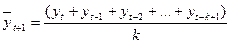 (15)
(15)
Где t - количество измерений,
yt - значение исследуемой характеристики в текущем периоде,
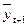 - прогнозное значение исследуемой характеристики на следующий период,
- прогнозное значение исследуемой характеристики на следующий период,
k - количество наблюдений в скользящем среднем. Величина k может принимать произвольно выбранное значение (3,4,5 и т.д.). Заметим, что величина k зависит от размера изучаемой совокупности, чем большее количество наблюдений анализируется, тем большее значение она может принимать.
Прогнозом на следующий период принимается скользящее среднее за предыдущий период.
Метод простого скользящего среднего может быть применен к стабильным данным, при незначительных колебаниях. В случае однонаправленных изменений исследуемого показателя (повышения или понижения) более точный прогноз может быть получен методом двойного скользящего среднего.
Метод двойного скользящего среднего представляет более сложную двухэтапную процедуру усреднения. Сначала временной ряд сглаживается методом простого скользящего среднего (формула 15), а потом повторяется процедура усреднения для рассчитанных значений (16).
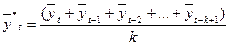 (16)
(16)
где 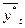 - вторичное скользящее среднее.
- вторичное скользящее среднее.
Для построения прогноза рассчитываются сумма первичного скользящего среднего и разницы между первичным и вторичным скользящим средним a (17) и коэффициент корректировки b (18)
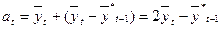 (17)
(17)
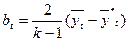 (18)
(18)
Прогнозное значение на p периодов вперед определяется по формуле (19)
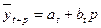 ……………..(19)
……………..(19)
Пример
На основе исходной информации о валютном курсе руб/долл. Требуется построить прогноз валютного курса на следующий месяц.
Рассмотрим результаты расчетов следующими методами:
· Простого среднего
· Скользящего среднего
· Двойного скользящего среднего.
Таблица 7
Расчет скользящей средней
| T | yt | 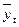
| et |
| 31,819 | |||
| 31,685 | |||
| 31,444 | |||
| 31,204 | 31,649 | 0,445 | |
| 31,907 | 31,444 | -0,463 | |
| 30,469 | 31,518 | 1,049 | |
| 30,360 | 31,193 | 0,833 | |
| 30,349 | 30,912 | 0,563 | |
| 30,599 | 30,393 | -0,206 | |
| 30,165 | 30,436 | 0,271 | |
| 29,808 | 30,371 | 0,563 | |
| 29,433 | 30,191 | 0,758 |
Прогнозное значение, рассчитанное по простой средней 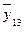 = 30,770 руб/долл
= 30,770 руб/долл
Прогнозное значение, рассчитанное по скользящей средней (при k=3) 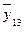 = 29,802 руб/долл , дисперсия D = 2,078, среднеквадратическое отклонение σ = 1,44 руб/долл.
= 29,802 руб/долл , дисперсия D = 2,078, среднеквадратическое отклонение σ = 1,44 руб/долл.
Таблица 8
Расчет двойной скользящей средней
| T | yt | 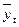
| 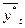
| A | b | a+bp | E |
| 31,819 | |||||||
| 31,685 | |||||||
| 31,444 | 31,649 | ||||||
| 31,204 | 31,444 | ||||||
| 31,907 | 31,518 | 31,537 | 31,499 | -0,019 | |||
| 30,469 | 31,193 | 31,385 | 31,001 | -0,192 | 31,480 | 1,011 | |
| 30,360 | 30,912 | 31,208 | 30,616 | -0,296 | 30,809 | 0,449 | |
| 30,349 | 30,393 | 30,833 | 29,953 | -0,440 | 30,320 | -0,029 | |
| 30,599 | 30,436 | 30,580 | 30,292 | -0,144 | 29,513 | -1,086 | |
| 30,165 | 30,371 | 30,400 | 30,342 | -0,029 | 30,148 | -0,017 | |
| 29,808 | 30,191 | 30,333 | 30,049 | -0,142 | 30,313 | 0,505 | |
| 29,433 | 29,802 | 30,121 | 29,483 | -0,319 | 29,207 | 0,474 |
Прогнозное значение, рассчитанное по скользящей средней (при k=3, р = 1), 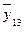 = 29,164 руб/долл , дисперсия D= 0,244, σ =0,48 руб/долл.
= 29,164 руб/долл , дисперсия D= 0,244, σ =0,48 руб/долл.
Дата добавления: 2016-04-22; просмотров: 5982;
