Элементарные функции прогнозной экстраполяции
| Вид функции | Алгоритм | График функции |
    1. Линейная 1. Линейная
| 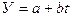
| у b>0 а b<0 0 t |
      2. Парабола 2. Парабола
| 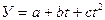
| у c>0 c = 0 а c< 0 0 t а / 2с |
3.   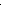 Кубическая
парабола Кубическая
парабола
| 
| У А 0 t |
     4. Степенная 4. Степенная
| У=аt b | у b> 1 b = 1 b< 1 0 t |
   5.Экспоненциальная 5.Экспоненциальная
| У=ае bt | У a 0 t |
    6. Модифицированная экспоненциальная 6. Модифицированная экспоненциальная
| У=k-a e bt | У K k-a 0 t |
7.         Логическая
(S-образная кривая) Логическая
(S-образная кривая)
|
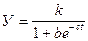
| у k k/2 k/1+b 0 t |
    8. Гиперболическая 8. Гиперболическая
|
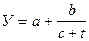
| У a+b/c a 0 t |
   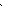 9. Колебательная 9. Колебательная
|
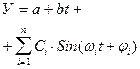
| У а t |
В социально- экономическом прогнозировании различают следующие типы динамики:
1. Равномерное развитие, под которым понимают экономический рост с постоянным абсолютным приростом. Анализируемый показатель изменяется за каждый временной интервал на одинаковую по абсолютному значению величину. Данный тип динамики может быть описан линейной функцией (30).
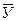 t = a + b * t (30),
t = a + b * t (30),
где а - теоретическое значение yt в точке отсчета, t = 0,
b - коэффициент регрессии, определяющий направление развития исследуемой характеристики,
- если b>0 - уровни ряда динамики равномерно возрастают,
- если b<0 - уровни ряда динамики равномерно убывают,
- если b = 0 - уровни ряда неизменны во времени.
2. Равноускоренное (равнозамедленное) развитие, под которым понимают экономический рост с постоянными темпами прироста. Данный тип динамики может быть описан функцией параболы второго порядка, показательной или экспоненциальной функциями. Уравнение параболической функции имеет следующий вид:
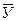 t = a +b * t + c * t2 (31),
t = a +b * t + c * t2 (31),
c - характеризует постоянное изменение интенсивности развития ( в единицу времени), если с > 0, то для процесса характерно ускорение динамики, если с < 0 - замедление. При этом параметр b может принимать положительные или отрицательные значения.
3. Развитие с переменным ускорением (замедлением) может быть описано кубической параболой (32).
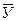 t = a + b * t +c * t2 +d * t3 (32)
t = a + b * t +c * t2 +d * t3 (32)
Наиболее распространенным способом выбора тренда является способ перебора различных функций и выбора наилучшей, исходя из значения принятого критерия. Обычно в качестве критерия принимают известные характеристики ошибки прогнозов, рассмотренные нами в предыдущей теме. Из совокупности функций выбирается та, которой соответствует минимальное значение принятого критерия, характеризующего ошибку прогноза.
Для нахождения параметров функции решаются определенные системы уравнений, которые приведены в таблице 8.
Таблица 8
Дата добавления: 2016-04-22; просмотров: 894;
