Початкові та крайові умови. Крайові задачі
Для того, щоб повністю описати той чи інший фізичний процес не достатньо мати лише рівняння, яке описує цей процес. Необхідно задати також початковий стан процесу, який описується початковими умовами та режим процесу на границі області моделювання, в якій протікає цей процес, що описується крайовими умовами. Математично це пов’язано з тим, що диференціальні рівняння мають безліч розв’язків. Дійсно, навіть для звичайного диференціального рівняння 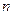 -го порядку загальний розв’язок залежить від
-го порядку загальний розв’язок залежить від 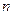 довільних сталих. Для рівнянь з частковими похідними, загальний розв’язок залежить, в загальному випадку, від довільних функцій. Тому, для того, щоб виділити потрібний розв’язок з множини можливих розв’язків, який описує заданий реальний фізичний процес, необхідно задати додаткові умови, а саме початкові та крайові умови. Часто початкові та крайові умови об’єднують одним поняттям, а саме крайовими умовами. Тоді відповідна задача, тобто задача знаходження розв’язку заданого диференціального рівняння, який задовольняє заданим крайовим умовам, називається крайовою задачею.
довільних сталих. Для рівнянь з частковими похідними, загальний розв’язок залежить, в загальному випадку, від довільних функцій. Тому, для того, щоб виділити потрібний розв’язок з множини можливих розв’язків, який описує заданий реальний фізичний процес, необхідно задати додаткові умови, а саме початкові та крайові умови. Часто початкові та крайові умови об’єднують одним поняттям, а саме крайовими умовами. Тоді відповідна задача, тобто задача знаходження розв’язку заданого диференціального рівняння, який задовольняє заданим крайовим умовам, називається крайовою задачею.
Важливим питанням є скільки початкових та крайових умов потрібно накласти, щоб отримати єдиний розв’язок крайової задачі? Якщо в диференціальне рівняння входить похідна по часу 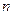 -го порядку, то початкових умов має бути
-го порядку, то початкових умов має бути 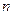 і задаються вони на шукану функцію та її похідні по часу до
і задаються вони на шукану функцію та її похідні по часу до 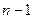 порядку включно. Найвищий порядок похідної за просторовими координатами визначає кількість крайових умов, які потрібно задати в кожній точці границі. Так, якщо цей порядок рівний
порядку включно. Найвищий порядок похідної за просторовими координатами визначає кількість крайових умов, які потрібно задати в кожній точці границі. Так, якщо цей порядок рівний 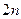 , то в кожній точці границі необхідно задати
, то в кожній точці границі необхідно задати 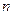 крайових умов.
крайових умов.
Крайовою умовою будемо називати значення шуканої функції на границі області моделювання. Розрізняють три типи крайових умов:
1) крайова умова І роду:
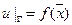 , (4.19)
, (4.19)
2) крайова умова ІІ роду:
 , (4.20)
, (4.20)
3) крайова умова ІІІ роду:
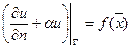 , (4.21)
, (4.21)
де  - деяка задана функція.
- деяка задана функція.
Необхідно зауважити, що задана функція може бути рівною константі.
Узагальнюючи, граничні умови (4.19 – 4.21) можна записати наступним чином:
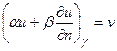 (4.22)
(4.22)
де  і
і 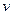
 - задані кусково-неперервні функції. Тоді умова (4.19) слідує з (4.22) як частковий випадок при
- задані кусково-неперервні функції. Тоді умова (4.19) слідує з (4.22) як частковий випадок при 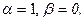 умова (4.20) – при
умова (4.20) – при 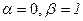 і умова (4.21) – при
і умова (4.21) – при  .
.
Необхідно зауважити, що при аналізі теплових процесів використовується ще четверта та п’ята крайові умови, хоча їх можна побудувати на основі існуючих (4.19 – 4.22).
Усі рівняння в часткових похідних можна розділити на стаціонарні та нестаціонарні. Диференціальне рівняння в часткових похідних, розв’язок якого змінюється в часі, називається нестаціонарним.
На відміну від розв’язку стаціонарних задач (РЧП та краєві умови) розв’язок нестаціонарних задач потребує додаткової компоненти, а саме початкової умови.
Початковою умовою називають значення функції в початковий момент часу, тобто при 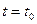 , яку можна записати:
, яку можна записати:

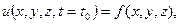
а у випадку, коли в РЧП присутня друга похідна за часом, то необхідно додати ще одну початкову умову:
 при
при 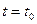 .
.
Дата добавления: 2016-04-22; просмотров: 651;
