Поняття про класичні та узагальнені розв’язки крайових задач
Розглянуті крайові задачі характеризуються тим, що їх розв’язки повинні бути достатньо гладкими і задовольняти рівняння в кожній точці області завдання цього рівняння. Такі розв’язки прийнято називати класичними, а постановку відповідної крайової задачі – класичною постановкою. Класичні постановки накладають досить жорсткі вимоги стосовно гладкості даних та розв’язків, наприклад, для розглянутих крайових задач, класичний розв’язок повинен бути двічі неперервно диференційованих в області задання. Однак, на практиці для цілого ряду важливих випадків вхідні дані можуть мати особливості або як прийнято казати бути сингулярними. Тому в таких випадках класичних постановок задач може бути недостатньо. Для того, щоб здійснити постановки таких задач доводиться відмовлятися (частково або повністю) від вимог гладкості розв’язку в області. Дана проблема вирішується шляхом введення поняття так званих узагальнених розв’язків, які базуються на понятті узагальнених функцій.
Узагальнена функція є узагальненням класичного поняття функції. Це узагальнення, з однієї сторони, дає можливість виразити в математичній формі такі ідеалізовані поняття, як густина матеріальної точки, густина заряду, інтенсивність миттєвого точкового джерела і т.д. З іншого боку, в понятті узагальненої функції знаходить відображення той факт, що реально неможливо, наприклад, виміряти густину речовини в точці, а можна виміряти лише середню густину в достатньо малому околі цієї точки. Грубо узагальнюючи, можна сказати, що узагальнена функція визначається своїми “середніми значеннями” в околі точки.
Математично строго узагальнена функція визначається як довільний лінійний неперервний функціонал на деякому просторі основних функцій, тобто узагальнена функція ставить у відповідність деякій “класичній” функції, в загальному випадку, комплексне число. Прикладом узагальненої функції може бути добре відома  - функція Дірака.
- функція Дірака.
Наведемо приклад постановки крайової задачі, що описує теплові процеси. Отже, визначити диференціальне рівняння для обчислення температурного поля та поставити початкову і крайові умови для поданої нижче задачі (див. рис. 4.1). Задано двовимірну область W (АВСД), температуру на границях АВ, АД та ДС (границя ВС є теплоізольованою), джерело тепла розміщене в центрі області і підтримується при постійній температурі 100 °С, в усіх внутрішніх точках області та на границі ВС в початковий момент часу температура рівна нулю ( 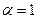 ), крок рівномірний, (
), крок рівномірний, (  ,
,  ).
).
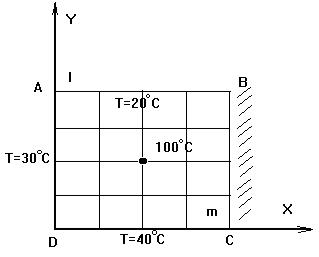
|
| Рис.4.1. Приклад області моделюванн крайової задачі |
Розв’язання задачі. Область моделювання наведено на рис.4.1. Це є двовимірна область у формі прямокутника ABCD, що залежить від двох просторових координат, а саме:  і
і  . Розподіл температури в області описується диференціальним рівнянням теплопровідності (Фур’є):
. Розподіл температури в області описується диференціальним рівнянням теплопровідності (Фур’є):

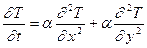 , (4.29)
, (4.29)
де 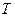 - температура;
- температура; 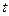 - час;
- час;  і
і 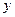 - просторові координати, а a - коефіцієнт температуропровідності.
- просторові координати, а a - коефіцієнт температуропровідності.
Для завершення математичної формалізаціїт задачі до рівняння (4.29) необхідно додати початкову та крайові умови.
Початкова умова має наступну форму:
 , (4.30)
, (4.30)
а краєві умови:
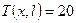 °C, де
°C, де 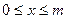 ; (4.31)
; (4.31)
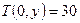 °C, де
°C, де 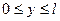 ;
;
 °C, де
°C, де 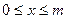 ;
;
 °C.
°C.
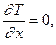 при
при 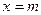 ,
, 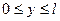 .
.
Сформульована крайова задача (4.29 – 4.31) дає змогу провести аналіз перехідного процесу. При нехтуванні перехідним процесом можна скористатися стаціонарним рівнянням наступного виду  з крайовими умовами (4.31).
з крайовими умовами (4.31).
Дата добавления: 2016-04-22; просмотров: 562;
