Поняття про коректність постановок крайових задач
Оскільки крайові задачі є математичними моделями реальних фізичних процесів, то їх постановки повинні задовольняти наступним, цілком природнім, вимогам:
1) розв’язок крайової задачі має існувати в деякому класі функцій 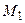 ;
;
2) розв’язок крайової задачі повинен бути єдиним в деякому класі функцій 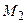 ;
;
3) розв’язок крайової задачі повинен неперервно залежати від даних задачі (початкових та граничних умов, вільного члена, коефіцієнтів рівняння).
Неперервна залежність розв’язку крайової задачі 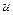 від деякого даного цієї задачі
від деякого даного цієї задачі 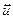 означає наступне: нехай послідовність даних
означає наступне: нехай послідовність даних 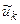 збігається до
збігається до  при
при 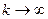 і
і  – відповідні розв’язки задачі; тоді
– відповідні розв’язки задачі; тоді  при
при 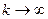 . Наприклад, якщо вихідну задачу можна представити у вигляді операторного рівняння
. Наприклад, якщо вихідну задачу можна представити у вигляді операторного рівняння  , де
, де 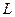 – лінійний оператор, то неперервна залежність розв’язку
– лінійний оператор, то неперервна залежність розв’язку 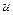 від вільного члена
від вільного члена 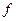 буде забезпечена, тоді коли обернений оператор
буде забезпечена, тоді коли обернений оператор  існує і він обмежений.
існує і він обмежений.
Вимога неперервної залежності розв’язку крайової задачі обумовлена тим, що фізичні дані, як правило, визначаються з експерименту наближено. Тому потрібно гарантувати, що розв’язок задачі в рамках вибраної математичної моделі не буде суттєво залежати від похибок вимірювання.
Задача, розв’язок якої задовольняє перераховані вище вимоги (1 – 3) називається коректно поставленою (за Адамаром [24]), а множина функцій 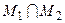 – класом коректності. Задача, розв’язок якої не задовольняє хоча б одній з вимог (1 – 3) називається некоректно поставленою.
– класом коректності. Задача, розв’язок якої не задовольняє хоча б одній з вимог (1 – 3) називається некоректно поставленою.
Вперше три умови коректності крайових задач математичної фізики сформулювали Д. Гільберт і Р. Курант [25]: існування, однозначна визначеність і неперервна залежність рішення від даних задачі. Відносно останнього сказано: “… воно має основне значення і зовсім не є тривіальним. … Математична задача тільки в тому випадку може вважатися адекватною для опису реальних явищ, якщо зміні запропонованих даних в достатньо тісних границях відповідає така ж мала, т.б. обмежена наперед заданими границями зміна рішення”.
Дата добавления: 2016-04-22; просмотров: 670;
