Класифікація диференціальних рівнянь з частинними похідними
Класифікація диференціальних рівнянь може здійснюватися за різними ознаками. Класифікація відіграє важливу роль, оскільки для кожного класу рівнянь розроблені відповідна теорія та методи розв’язування. Основними критеріями класифікації ДРЧП є:
1) Порядок рівняння. Порядком рівняння є найвищий порядок похідної, що входить в це рівняння. Наприклад,
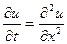 – рівняння 2-го порядку,
– рівняння 2-го порядку,
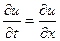 – рівняння 1-го порядку.
– рівняння 1-го порядку.
Найпоширенішими є ДРЧП 2-го порядку.
2) Число незалежних змінних. Незалежними змінними є змінні від яких залежить невідома (шукана) функція. На практиці в ролі незалежних змінних виступають звичайні Декартові координати у просторі та час. Наприклад, диференціальне рівняння (4.16) має дві незалежні змінні  та
та 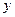 , диференціальне рівняння (4.14) – три (
, диференціальне рівняння (4.14) – три ( 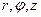 ).
).
3) Лінійність. Розрізняють лінійні та нелінійні рівняння з частинними похідними. У лінійних рівняннях залежна змінна (функція) та всі її похідні входять лінійно, тобто вони не перемножуються, не підносяться до квадрату, не є аргументами інших функцій і т.д. У протилежному випадку рівняння буде нелінійним. Приклади нелінійних рівнянь наведено нижче:
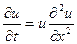 ,
,
або
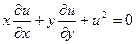 .
.
В загальному випадку, лінійним рівнянням другого порядку з двома незалежними змінними називається рівняння такого виду
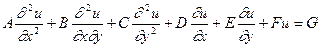 , (4.18)
, (4.18)
де 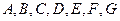 - задані функції змінних
- задані функції змінних  та
та 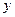 .
.
4) Однорідність.Диференціальне рівняння називається однорідним, якщо вільний член тотожньо дорівнює нулю в заданій області визначення. У протилежному випадку рівняння називається неоднорідним. Наприклад, рівняння Пуассона – неоднорідне, а рівняння Лапласа –однорідне.
5) Вид коефіцієнтів. Якщо коефіцієнти рівняння є сталими величинами, то таке рівняння називається рівнянням з постійними коефіцієнтами, у протилежному випадку – рівнянням зі змінними коефіцієнтами.
Усі лінійні ДРЧП другого порядку відносяться до одного з трьох типів: параболічного, гіперболічного та еліптичного. Рівняння параболічного типу визначаються умовою (в термінах формули (4.18)) 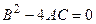 . Рівняння дифузії (та всі його часткові випадки) має параболічний тип. Рівняння гіперболічного типу описують коливальні процеси і визначаються умовою
. Рівняння дифузії (та всі його часткові випадки) має параболічний тип. Рівняння гіперболічного типу описують коливальні процеси і визначаються умовою 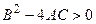 . Рівняння еліптичного типу описують встановлені процеси і задаються умовою
. Рівняння еліптичного типу описують встановлені процеси і задаються умовою 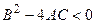 . Зокрема, рівняння Пуассона і Лапласа є еліптичними. У випадку змінних коефіцієнтів тип рівняння може змінюватися від точки до точки.
. Зокрема, рівняння Пуассона і Лапласа є еліптичними. У випадку змінних коефіцієнтів тип рівняння може змінюватися від точки до точки.
6) Стаціонарність. Якщо ДРЧП включає похідну по часу, то таке диференціальне рівняння називається нестаціонарним в іншому випадку – стаціонарним. Приклади стаціонарних ДРЧП є (4.13), (4.14) та (4.16), а приклади нестаціонарних – (4.2) – (4.8).
Дата добавления: 2016-04-22; просмотров: 851;
