Основні рівняння для моделей на компонентному рівні

Математичні моделі на компонентному рівні проектування для багатьох фізичних процесів описуються диференціальними рівняннями з частинними похідними (ДРЧП). Важливий клас диференціальних рівнянь з частинними похідними [5] складають лінійні рівняння другого порядку з 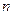незалежними змінними, які в загальному випадку можна записати наступним чином:

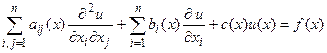. (4.1)

Найбільш поширеними частковими випадками рівняння (4.1) є: рівняння коливань, рівняння дифузії та стаціонарні рівняння.

Рівняння коливань має вигляд:

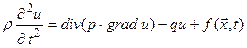, (4.2)

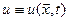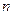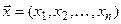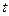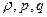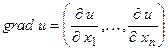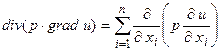де невідома функція залежить від просторових координат і часу , коефіцієнти визначаються властивостями середовища, в якому відбувається коливальний процес, функція виражає інтенсивність зовнішніх впливів, , . Рівняння (4.2) описує такі фізичні процеси як коливання струни, мембрани, тривимірних тіл, електромагнітні коливання і т.д. З рівняння (4.2), як частковий випадок, можна отримати класичне хвильове рівняння:

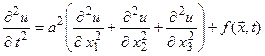, (4.3)

яке описує процеси поширення звуку та електромагнітних хвиль в однорідному середовищі. У двовимірному випадку хвильове рівняння (4.3) описує малі поперечні коливання мембрани, а в одновимірному – такі фізичні процеси, як поперечні коливання струни та повздовжні коливання пружного стрижня. Ввівши оператор Лапласа

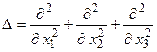
тоді хвильове рівняння (4.3) можна записати так

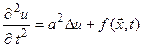. (4.4)

Рівняння дифузії

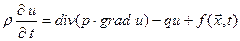(4.5)

описує процеси поширення тепла або дифузії частинок у деякому середовищі, яке характеризується парметрами 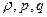. Як частковий випадок, з рівняння (4.5) можна отримати класичне рівняння теплопровідності

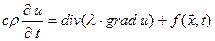, (4.6)

де 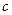– питома теплоємність, 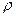– густина, 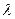– коефіцієнт теплопровідності середовища, в якому відбувається процес поширення тепла, – інтенсивність внутрішніх джерел тепла. Якщо середовище є ізотропним, тобто 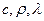– константи, то з рівняння (4.6) отримаємо

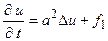, (4.7)

де 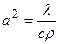називається коефіцієнтом температуропровідності, 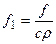– густина джерел тепла. Якщо внутрішні джерела тепла відсутні, тобто 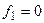, то з рівняння (4.7) отримаємо класичне рівняння Фур’є

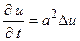. (4.8)

Стаціонарні рівняння описують встановлені процеси, в яких величини, що характеризують їх не залежать від часу. Тоді рівняння коливань (4.2) та дифузії (4.5) будуть мати вигляд:

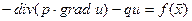. (4.9)

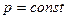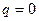При і рівняння (4.9) набуває вигляду

, (4.10)

і називається рівнянням Пуассона, а при 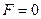отримуємо частковий випадок рівняння Пуассона, а саме рівняння Лапласа

. (4.11)

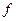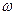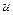Встановлені періодичні процеси, тобто, процеси, в яких зовнішні збурення є періодичними з частотою і амплітудою і шукана функція є також періодичною, описуються рівнянням Гельмгольца

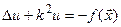, (4.12)

де 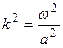, а невідома функція 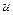буде трактуватися як амплітуда коливань. Рівняння Гельмгольца описує також процеси розсіювання та дифракції.

Рівняння Лапласа (4.11) на практиці зустрічається дуже часто, тому важливо мати його вигляд у різних системах координат. У сферичній системі координат ( , , 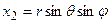) рівняння Лапласа набуває вигляду

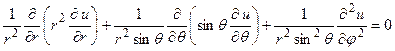, (4.13)

а у циліндричній системі координат ( 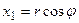, , ) – вигляду

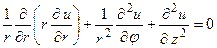. (4.14)

Іншими прикладами рівнянь, які відіграють важливу роль у математичному моделюванні різноманітних фізичних процесів та явищ є:

a) телеграфне рівняння (описує розподіл електричного струму в провіднику):

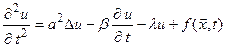; (4.15)

b) бігармонійне рівняння (описує коливання пружних тіл, таких як балка, пластина і т.д.):

, (4.16)

c) рівняння на власні значення (дає змогу визначати резонансні частоти коливань):

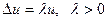. (4.17)