Представление в пространстве состояний

Представление задач в пространстве состояний включает описание всех состояний или только начальных, задание операторов, отображающих одни состояния в другие, и задание целевого состояния. Возможны различные формы описания состояний задачи. В частности, могут быть использованы строки, векторы, матрицы, графы. Форму описания состояний задачи выбирают так, чтобы применение оператора, преобразующего одно состояние в другое, было достаточно простым.

Операторы могут быть заданы с помощью таблицы, связывающей каждое входное состояние с некоторым выходным. Для больших задач такое задание оператора практически непригодно. При описании состояний в форме строки (вектора) оператор удобно задавать в виде правил переписывания.

Процедура поиска решения в пространстве состояний заключается в том, чтобы найти последовательность операторов, преобразующих начальное состояние в целевое. Решением задачи является указанная последовательность операторов.

Представление задачи в пространстве состояний определяется совокупностью трех составляющих – ( S₀, F, G), где S₀ – множество начальных состояний; F – множество операторов, отображающих одно состояние в другое (т.е. пространство состояний в себя); G – множество целевых состояний.

Рассмотрим примеры представления задач в пространстве состояний.

1. Задача о выборе маршрута или задача о коммивояжере.

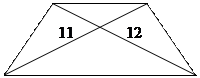
Транспортный робот должен построить маршрут так, чтобы побывать в каждом из n заданных пунктов по одному разу и возвратиться в исходный пункт. При этом, если таких маршрутов несколько, надо выбрать маршрут минимальной протяженности. На рис. 8.1 приведена схема расположения пунктов A, B, C, D, маршрутов и расстояний.

А 5 В

6 10

С 8 D

Рис. 8.1 Схема маршрутов.

Состояния в этой задаче можно задавать строкой, обозначающей список пунктов, пройденных к текущему моменту. Если начальный пункт А, то начальное состояние задается строкой из одной буквы А. Не допускается, чтобы в строке какой-либо пункт упоминался более одного раза. Исключением является строка, соответствующая целевому состоянию, в которой в конце повторно указывается исходный пункт после перечисления всех остальных пунктов.

Операторы – это отображения, соответствующие решению робота направиться из данного пункта в какой-либо следующий.

Целевым состоянием, если не требуется минимизировать протяженность маршрута, является любое состояние, описание которого начинается и заканчивается A и содержит названия всех других пунктов. Таким, например, является состояние ABCDA.

Задача о манипуляции предметами.

Пусть состояние (мир) задачи включает некоторое число площадок с расположенными на них блоками, а также робот - манипулятор, перемещающий блоки с одной площадки на другую и устанавливающий их друг на друга.

Текущее состояние задачи можно интерпретировать как текущее расположение блоков на площадках. Способы перемещения блоков роботом, т.е. переход из одного состояния в другое, подчиняются некоторым требованиям. Так, может быть ограничено число блоков на конкретной площадке, для перемещения следует выбирать блоки, лежащие сверху, и т.д. На основе таких требований строится множество F допустимых операторов перехода, которые представляют совокупность разрешенных действий робота. Желаемое расположение блоков на площадках есть целевое состояние задачи. Решением задачи является последовательность операторов F₁,…, F_n, с помощью которой можно переставить блоки из некоторого начального расположения (начального состояния) в желаемое, т.е. целевое состояние.

При описании пространства состояний и методов поиска решений широко используется граф и особенно одна его разновидность, называемая деревом.

Дерево – это ориентированный граф, в каждую вершину которого входит только одна дуга, за исключением одной вершины, называемой корнем дерева. В корень не входит ни одна дуга. Если 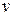– какая-либо вершина дерева и вершины 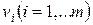являются концами дуг, выходящих из вершины 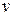, то говорят, что вершина 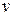порождает вершины .

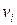Введем понятие уровня. Будем считать, что корень находится на нулевом уровне; вершины, порожденные корнем, – на первом уровне; вершины, порожденные вершинами к- го уровня, находятся на 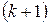- м уровне.