Алгоритм полного перебора

Вершины раскрываются в том порядке, в котором они были порождены. Первой раскрывается начальная вершина. Проверяется среди порожденных вершин наличие целевой. Если есть, поиск заканчивается. Если нет, то раскрывается первая из порожденных вершин и проверяется наличие целевых вершин. Затем раскрывается вторая из порожденных вершин и т.д.

Для записи алгоритмов поиска в пространстве состояний введем понятия списков открытых (ОТК) и закрытых (ЗКР) вершин. Список закрытых вершин – это список, где размещаются идентификаторы раскрытых вершин и идентификатор вершины, которую предстоит раскрыть в данный момент. Вершины из списка ЗКР, кроме последней, раскрывать нельзя. Список открытых вершин – это список, где размещаются идентификаторы вершин, которые могут и должны быть раскрыты.

Стратегии поиска различаются правилами размещения вершин в списке ОТК и выбора очередной вершины для раскрытия.

Алгоритм полного перебора включает следующие шаги.

1. Поместить начальную вершину в список ОТК.

2. Если список ОТК пуст, выдать сообщение о неудаче поиска, иначе перейти к следующему шагу.

3. Взять первую вершину из списка ОТК и перенести ее в список ЗКР, присвоить вершине идентификатор .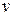

4. Раскрыть вершину 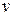. Поместить все дочерние неповторяющиеся (т.е. не встречающиеся в списке ЗКР) вершины в конец списка ОТК и построить указатели, ведущие от них к вершине 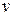. Если вершина 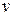не имеет дочерних вершин, то перейти к шагу 2.

5. Проверить, не является ли одна из дочерних вершин 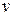целевой. Если является, то выдать решение, в ином случае перейти к шагу 2.

В этом алгоритме предполагается, что начальная вершина не может быть

целевой. Алгоритм позволяет найти оптимальное (минимальное по числу дуг) решение. Например, использование этого алгоритма для решения задачи о выборе маршрута (минимальной длины) сводится к построению графа состояний (см. рис. 8.3). Имея этот граф и сравнивая длины различных маршрутов, ведущих к целевым состояниям, можно выбрать оптимальные маршруты. Как следует из графа состояний, таких маршрутов два – маршруты, ведущие к целевым состояниям ABCDA и ADCBA.