Алгоритмы упорядоченного перебора

Для большинства практических задач удается сформулировать эмпирические правила, позволяющие уменьшить объем перебора. Эти правила используют специфическую информацию о решаемой задаче, формируемую на основе опыта, интуиции и здравого смысла исследователя. Информацию такого рода называют эвристической, а основанные на ней алгоритмы – эвристическими.

Основная идея эвристических алгоритмов заключается в упорядочении списка открытых вершин в соответствии с некоторой мерой, оценивающей «перспективность» вершины или пути, на котором находится данная вершина. Такую меру называют оценочной функцией. Для очередного раскрытия из списка ОТК выбирается вершина, имеющая минимальное значение оценочной функции. После каждого шага раскрытия производится переупорядочивание вершин в списке в соответствии со значениями оценочной функции. Процедуру такого типа называются алгоритмом упорядоченного перебора.

Существуют различные идеологии построения оценочных функций. Рассмотрим наиболее распространенную.

Пусть 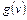– стоимость кратчайшего (оптимального) пути из любой начальной вершины 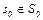до некоторой вершины 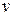. Стоимость кратчайшего пути из вершины 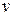до ближайшей целевой вершины 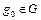обозначим 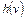. Функция 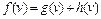выражает стоимость кратчайшего пути из начальной вершины в целевую при условии, что он проходит через вершину .

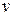Введем следующие оценочные функции:

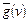– оценка стоимости кратчайшего пути из начальной вершины в вершину ;

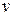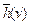– оценка стоимости кратчайшего пути из вершины 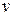до ближайшей целевой.

Тогда функция

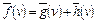(8.1)

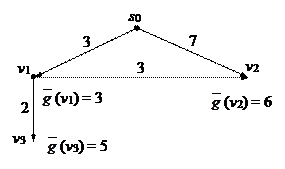
является оценкой функции 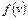, т.е. оценкой стоимости кратчайшего пути из начальной вершины в целевую при условии, что он проходит через вершину 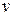. В качестве значения функции 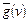естественно выбрать действительную стоимость пути из начальной вершины в вершину 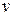, найденного алгоритмом перебора к данному моменту. Заметим, что если граф состояний не имеет структуру дерева, то значение 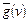может меняться в процессе раскрытия вершин. Поясним это на примере (рис. 8.6).

a) б)

Рис. 8.6 Граф состояний, не имеющий структуру дерева

Пусть на шаге 1 поиска раскрыта вершина s₀ и порождены вершины v₁ и v₂ со значениями стоимосте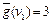й и 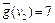(рис.8.6,а). На шаге 2 раскрывается вершина v₁ и порождаются вершина v₃ и снова вершина v₂, причем из v₁ в v₂ ведет путь стоимостью 3 (рис. 8.6,б). Очевидно, стоимость кратчайшего пути из s₀ в v₂ равна .

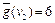Как следует из определения и приведенного примера, 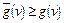. Оценочная функция 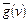вычисляется в процессе работы алгоритма перебора.

При построении оценочной функции 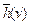опираются на любую эвристическую информацию о решаемой задаче, поэтому 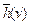называют эвристической функцией. Если 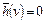, то алгоритм перебора сводится к алгоритму равных цен, что соответствует полному отсутствию эвристической информации.

Не существует общих рекомендаций к способам определения функции 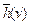, поэтому рассмотрим ее смысл на примере. Конкретизируем задачу о манипуляции предметами следующим образом. Три пронумерованных блока располагаются на трех площадках. Робот может перемещать с одной площадки на другую по одному блоку. Блоки могут устанавливаться друг на друга. Для перемещения можно брать только верхний блок. Заданы начальное и целевое расположение блоков. Задача заключается в определении плана перемещения блоков, позволяющего за минимальное число шагов (шаг – одно перемещение блока) перейти от начального расположения к целевому. На рис. 8.7 представлены целевое и начальное расположение блоков на площадках.

Начальное состояние Целевое состояние

Рис. 8.7 Расположение блоков на площадках

В качестве эвристической функции 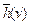примем сумму числа блоков, расположенных не на своем месте, и общего числа блоков, препятствующих установке каждого из них на свое место. Препятствующими считаются блоки, расположенные сверху какого-либо блока, который надо переместить, и блоки, занимающие «чужие» места в целевой конфигурации, т.е. места, в которые должны быть установлены блоки, расположенные не на своем месте.

Граф решения задачи с помощью алгоритма упорядоченного перебора при указанной эвристической функции приведен на рис. 8.8. Для удобства вершины пронумерованы.

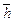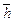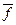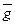Эвристическая функция вершины 1 равна (1) = 7, так как не на своем месте расположены два блока (2 и 3). Места, которые они должны занять, заняты другими блоками и над блоком 2 расположены два блока, а над блоком 3 – один ( (1) = 2 + 2 + 2 + 1 = 7). Поэтому оценочная функция (1) = (1) + 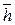(1) = 8. Аналогично считаются значения оценочной функции на других вершинах первого уровня.

Среди вершин первого уровня наименьшее значение функции 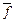имеет вершина 3. Поэтому на шаге 2 раскрывается эта вершина. При этом повторяющиеся

вершины не строятся и значения функции 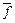таких вершин сохраняются, так как функция 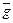с каждым шагом возрастает, а функция 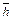не изменяется. На шаге 3 возникает задача выбора вершины для раскрытия, поскольку три вершины (5, 6 и 4) имеют минимальную оценку 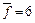. Условимся, что при одинаковых значениях 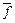предпочтение отдается тем вершинам, у которых меньше 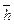. Вершины 5 и 6 имеют одинаковые значения 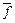и 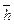. Граф на рис. 8.8 соответствует случаю, когда эти вершины упорядочены так, что сначала раскрывается вершина 5.

Рассмотрим некоторые свойства алгоритмов упорядоченного перебора. Алгоритм называют гарантирующим или допустимым, если для произвольного графа состояний он заканчивает работу построением оптимального пути.

Для сравнения эффективности алгоритмов перебора используется понятие эвристической силы. Пусть 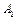и 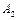– произвольные гарантирующие алгоритмы перебора, а 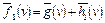, 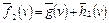– используемые ими оценочные функции. Алгоритм 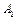называют эвристически более сильным, чем алгоритм 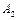, если на всех вершинах, кроме целевой, выполняется неравенство 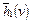> 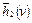. Эвристически более сильный алгоритм 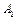раскрывает меньшее число вершин при поиске минимального пути, чем алгоритм 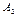. Обозначим 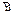– множество гарантирующих алгоритмов, которые можно использовать для решения данной задачи. Алгоритм 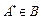называют оптимальным, если он не раскрывает большее число вершин, чем любой другой алгоритм .

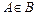Оптимальность в указанном смысле не является исчерпывающей характеристикой эффективности алгоритма, так как не учитывает сложность вычисления эвристической функции 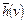. В большинстве практических задач более объективной характеристикой является оценка объема вычислений, необходимых для определения значений 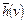на всех шагах к целевой вершине.

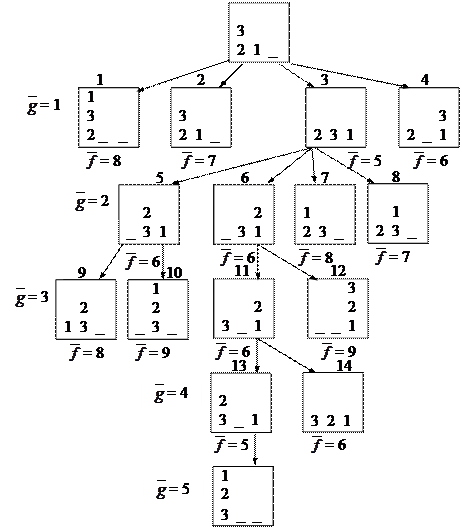Рис. 8.8 Граф решения задачи о манипуляции предметами